Τράπεζα Θεμάτων
www.trapeza-thematon.gr
| Τύπος Σχολείου: | Γενικό Λύκειο | Τάξη: | Α' Λυκείου |
|---|---|---|---|
| Μάθημα: | Γεωμετρία | Θέμα: | 2 |
| Κωδικός Θέματος: | 12636 | Ύλη: | 3.1. Είδη και στοιχεία τριγώνων 3.2. 1ο Κριτήριο ισότητας τριγώνων 3.4. 3ο Κριτήριο ισότητας τριγώνων |
| Τύπος Σχολείου: | Γενικό Λύκειο |
|---|---|
| Τάξη: | Α' Λυκείου |
| Μάθημα: | Γεωμετρία |
| Θέμα: | 2 |
| Κωδικός Θέματος: | 12636 |
| Ύλη: | 3.1. Είδη και στοιχεία τριγώνων 3.2. 1ο Κριτήριο ισότητας τριγώνων 3.4. 3ο Κριτήριο ισότητας τριγώνων |
| Τελευταία Ενημέρωση: 09-Οκτ-2021 | |
Θέμα 2
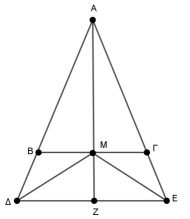
Δίνεται ισοσκελές τρίγωνο \(ΑΒΓ\) με \(ΑΒ=ΑΓ\) και \(Μ\) είναι το μέσο της βάσης \(ΒΓ\). Στις προεκτάσεις των πλευρών \(ΑΒ\), \(ΑΓ\) παίρνουμε τα τμήματα \(ΒΔ\), \(ΓΕ\) αντίστοιχα ώστε \(ΒΔ=ΓΕ\).
α) Να αποδείξετε ότι τα τρίγωνα \(ΜΒΔ\) και \(ΜΓΕ\) είναι ίσα.
(Μονάδες 12)
β) Να αποδείξετε ότι η γωνία \(ΜΔΕ\) είναι ίση με τη γωνία \(ΜΕΔ\).
(Μονάδες 6)
γ) Αν η \(ΑΜ\) τέμνει την \(ΔΕ\) στο σημείο \(Ζ\) να αποδείξετε ότι η \(ΑΖ\) είναι κάθετη στην \(ΔΕ\).
(Μονάδες 7)
Απάντηση Θέματος:
ΛΥΣΗ
α) Τα τρίγωνα \(ΜΒΔ\) και \(ΜΓΕ\) έχουν:
- \(ΜΒ = ΜΓ\), το \(Μ\) είναι μέσο της \(ΒΓ\)
- \(ΒΔ = ΓΕ\), από υπόθεση
- \(\hat{ΜΒΔ} = \hat{ΜΓΕ}\), ως παραπληρωματικές των ίσων γωνιών \(Β\) και \(Γ\)
άρα τα τρίγωνα \(ΜΒΔ\) και \(ΜΓΕ\) είναι ίσα (\(ΠΓΠ\)).
β) Λόγω του (α) είναι \(ΜΔ = ΜΕ\), γιατί βρίσκονται απέναντι από τις ίσες γωνίες \(\hat{ΜΒΔ}\) και \(\hat{ΜΓΕ}\) των ίσων τριγώνων \(ΜΒΔ\) και \(ΜΓΕ\) αντίστοιχα. Επομένως το τρίγωνο \(ΜΔΕ\) είναι ισοσκελές, οπότε οι γωνίες της βάσης του \(ΜΔΕ\) και \(ΜΕΔ\) είναι ίσες.
γ) Στο ισοσκελές τρίγωνο \(ΑΒΓ\) η \(ΑΜ\) είναι διάμεσος άρα και διχοτόμος. Επίσης \(ΑΔ = ΑΒ + ΒΔ\) και \(ΑΕ = ΑΓ +ΓΕ\), οπότε \(ΑΔ=ΑΕ\) ως άθροισμα ίσων τμημάτων. Έτσι στο ισοσκελές τρίγωνο \(ΑΔΕ\), η \(ΑΖ\) ως διχοτόμος θα είναι και ύψος. Άρα η \(ΑΖ\) είναι κάθετη στην \(ΔΕ\).
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida).