Τράπεζα Θεμάτων
www.trapeza-thematon.gr
| Τύπος Σχολείου: | Γενικό Λύκειο | Τάξη: | Α' Λυκείου |
|---|---|---|---|
| Μάθημα: | Φυσική | Θέμα: | 2 |
| Κωδικός Θέματος: | 13508 | Ύλη: | 1.3.6 Ισορροπία ομοεπιπέδων δυνάμεων 2.1.3 Η δυναμική ενέργεια 2.1.4 Η μηχανική ενέργεια |
| Τύπος Σχολείου: | Γενικό Λύκειο |
|---|---|
| Τάξη: | Α' Λυκείου |
| Μάθημα: | Φυσική |
| Θέμα: | 2 |
| Κωδικός Θέματος: | 13508 |
| Ύλη: | 1.3.6 Ισορροπία ομοεπιπέδων δυνάμεων 2.1.3 Η δυναμική ενέργεια 2.1.4 Η μηχανική ενέργεια |
| Τελευταία Ενημέρωση: 31-Μαρ-2022 | |
ΘΕΜΑ 2

2.1. Ο λόγος των μέτρων των ταχυτήτων με τις οποίες τα σώματα \(Α\) και \(Β\) του σχήματος, με μάζες \(𝑚\) και \(2𝑚\) αντίστοιχα, φθάνουν στο έδαφος είναι:
(Και στις δύο περιπτώσεις η αντίσταση του αέρα θεωρείται αμελητέα).
Α. Να επιλέξετε την σωστή απάντηση:
α. \(\dfrac{𝜐_𝛢}{𝜐_𝛣}=\sqrt{2}\)
β. \(\dfrac{𝜐_𝛢}{𝜐_𝛣}=1\)
γ. \(\dfrac{𝜐_𝛢}{𝜐_𝛣}=\dfrac{1}{\sqrt{2}}\)
Μονάδες 4
Β. Να δικαιολογήσετε την επιλογή σας.
Μονάδες 8
2.2. Το σώμα βάρους \(\vec{B}\) και στις τρεις περιπτώσεις, όπως φαίνονται στα παρακάτω σχήματα, ισορροπεί δεμένο στο αντίστοιχο νήμα ή στα νήματα. Για τα μέτρα των δυνάμεων \(𝐹_1\) , \(𝐹_2\), \(𝐹_3\), που δέχεται το σώμα από το νήμα ή τα νήματα ισχύει:
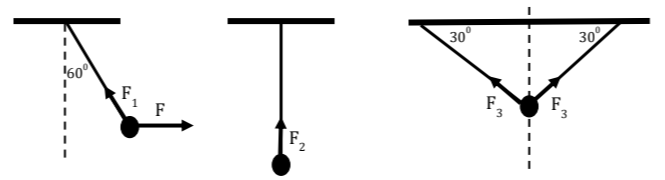
Δίνεται \(συν60^0 =\dfrac{1}{2}\)
Α. Να επιλέξετε την σωστή απάντηση:
α. \(𝐹_1> 𝐹_2>𝐹_3\)
β. \(𝐹_1> 𝐹_2=𝐹_3\)
γ. \(𝐹_1< 𝐹_2=𝐹_3\)
Μονάδες 4
Β. Να δικαιολογήσετε την επιλογή σας.
Μονάδες 9
Απάντηση Θέματος:
2.1
Α. Σωστή είναι η απάντηση (α).
(Μονάδες 4)
Β. Ενδεικτική δικαιολόγηση

Εφόσον θεωρούμε αμελητέα την αντίσταση του αέρα, δηλ. η μοναδική δύναμη που ασκείται σε κάθε σώμα είναι το βάρος του, άρα η Μηχανική Ενέργεια κάθε σώματος διατηρείται σταθερή.
(Μονάδα 1)
Για το σώμα Α έχουμε:
$$\begin{align}𝛫_{𝛼𝜌𝜒(𝛢)}+𝑈_{𝛼𝜌𝜒(𝛢)}&=𝛫_{𝜏𝜀𝜆(𝛢)}+𝑈_{𝜏𝜀𝜆(𝛢)}\\ \\0+𝑚𝑔ℎ&=\dfrac{1}{2}𝑚𝜐^2_𝛢+0\\ \\𝝊_𝜜&=\sqrt{𝟐𝒈𝒉}\end{align} \ (1)$$
(Μονάδες 3)
Για το σώμα B έχουμε:
$$\begin{align}𝛫_{𝛼𝜌𝜒(𝛣)}+𝑈_{𝛼𝜌𝜒(𝛣)}&=𝛫_{𝜏𝜀𝜆(𝛣)}+𝑈_{𝜏𝜀𝜆(𝛣)}\\ \\0+2𝑚𝑔\dfrac{ℎ}{2}&=\dfrac{1}{2}2𝑚𝜐^2_𝛣+0 \\ \\𝝊_𝜝&=\sqrt{𝒈𝒉 }\end{align} \ (2)$$
(Μονάδες 3)
Διαιρώντας τις \((1)\) και \((2)\) κατά μέλη προκύπτει:
$$\begin{align}\dfrac{𝜐_𝛢}{𝜐_𝛣}&=\dfrac{\sqrt{2𝑔ℎ}}{\sqrt{𝑔ℎ}}\\ \\\dfrac{𝜐_𝛢}{𝜐_𝛣}&=\sqrt{2}\end{align}$$
(Μονάδα 1)
2.2
Α. Σωστή είναι η απάντηση (β).
(Μονάδες 4)
Β. Ενδεικτική δικαιολόγηση:

Σχεδίαση δυνάμεων- Ανάλυση σε άξονες.
(Μονάδες 4)
Στην περίπτωση (1):
$$\begin{align}𝛴𝐹_𝑦&=0\\ \Rightarrow 𝐹_{1,𝑦}&=𝐵\\ \Rightarrow 𝐹_1𝜎𝜐𝜈60^0&=𝛣\\ \Rightarrow \dfrac{𝐹_1}{2}&=𝛣\\ \Rightarrow 𝑭_𝟏&=𝟐𝜝, \ (𝟏)\end{align}$$
(Μονάδες 2)
Στην περίπτωση (2):
$$\begin{align}𝛴𝐹_𝑦 &=0\\ \Rightarrow 𝑭_𝟐 & =𝑩, \ (𝟐)\end{align}$$
(Μονάδα 1)
Στην περίπτωση (3):
$$\begin{align}𝛴𝐹_𝑦&=0\\ \Rightarrow 2𝐹_{3,𝑦}&=𝐵\\ \Rightarrow 2𝐹_3\cdot 𝜎𝜐𝜈60^0 &=𝛣\\ \Rightarrow 2\dfrac{𝐹_3}{2}&=𝛣\\ \Rightarrow 𝑭_𝟑&=𝜝, \ (𝟑)\end{align}$$
(Μονάδες 2)
Άρα:
$$𝑭_𝟏> 𝑭_𝟐=𝑭_𝟑$$
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida).