Τράπεζα Θεμάτων
www.trapeza-thematon.gr
| Τύπος Σχολείου: | Γενικό Λύκειο | Τάξη: | Α' Λυκείου |
|---|---|---|---|
| Μάθημα: | Γεωμετρία | Θέμα: | 2 |
| Κωδικός Θέματος: | 13817 | Ύλη: | 3.15. Εφαπτόμενα τμήματα |
| Τύπος Σχολείου: | Γενικό Λύκειο |
|---|---|
| Τάξη: | Α' Λυκείου |
| Μάθημα: | Γεωμετρία |
| Θέμα: | 2 |
| Κωδικός Θέματος: | 13817 |
| Ύλη: | 3.15. Εφαπτόμενα τμήματα |
| Τελευταία Ενημέρωση: 31-Οκτ-2021 | |
ΘΕΜΑ 2
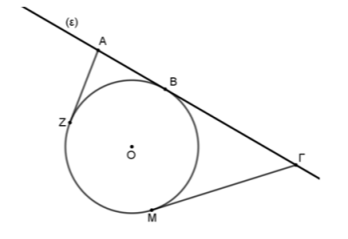
Δίνεται κύκλος με κέντρο \(Ο\) και ακτίνα \(ρ\). Σε σημείο \(Β\) του κύκλου φέρουμε εφαπτόμενη ευθεία \((ε)\). Θεωρούμε στην ευθεία \((ε)\) δύο σημεία \(Α\) και \(Γ\) εκατέρωθεν του \(Β\) έτσι ώστε \(ΒΑ < ΒΓ\) και από τα σημεία αυτά, φέρουμε τα εφαπτόμενα τμήματα \(ΑΖ\) και \(ΓΜ\) στον κύκλο.
α) Να γράψετε τα ευθύγραμμα τμήματα τα οποία είναι ίσα, αιτιολογώντας την απάντησή σας.
(Μονάδες 15)
β) Να αποδείξετε ότι \(ΑΓ = ΑΖ + ΜΓ\).
(Μονάδες 10)
Απάντηση Θέματος:
ΛΥΣΗ
α) Από τα δεδομένα τα ευθύγραμμα τμήματα \(ΑΒ\) και \(ΑΖ\) είναι εφαπτόμενα στον κύκλο από σημείο εκτός αυτού, άρα είναι ίσα, δηλαδή \(ΑΒ = ΑΖ\). Όμοια από το σημείο \(Γ\) που είναι εκτός του κύκλου τα ευθύγραμμα τμήματα \(ΓΒ\), \(ΓΜ\) είναι εφαπτόμενα σε αυτόν, άρα \(ΓΒ=ΓΜ\).
β) Λόγω του ερωτήματος (α) έχουμε \(ΑΓ = ΑΒ + ΒΓ = ΑΖ + ΜΓ\).
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida).