Τράπεζα Θεμάτων
www.trapeza-thematon.gr
| Τύπος Σχολείου: | Γενικό Λύκειο | Τάξη: | Α' Λυκείου |
|---|---|---|---|
| Μάθημα: | Φυσική | Θέμα: | 4 |
| Κωδικός Θέματος: | 14527 | Ύλη: | 1.1.9. Οι εξισώσεις προσδιορισμού της ταχύτητας και της θέσης ενός κινητού στην ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 1.2.4 Ο δεύτερος νόμος του Νεύτωνα ή Θεμελιώδης νόμος της Μηχανικής 2.1.1 Η έννοια του έργου 2.1.2 Έργο βάρους και μεταβολή της κινητικής ενέργειας |
| Τύπος Σχολείου: | Γενικό Λύκειο |
|---|---|
| Τάξη: | Α' Λυκείου |
| Μάθημα: | Φυσική |
| Θέμα: | 4 |
| Κωδικός Θέματος: | 14527 |
| Ύλη: | 1.1.9. Οι εξισώσεις προσδιορισμού της ταχύτητας και της θέσης ενός κινητού στην ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 1.2.4 Ο δεύτερος νόμος του Νεύτωνα ή Θεμελιώδης νόμος της Μηχανικής 2.1.1 Η έννοια του έργου 2.1.2 Έργο βάρους και μεταβολή της κινητικής ενέργειας |
| Τελευταία Ενημέρωση: 15-Απρ-2024 | |
ΘΕΜΑ 4
Ένα σώμα μάζας \(𝑚=10 Kg\) κινείται πάνω σε λείο οριζόντιο επίπεδο. Το διάγραμμα της ταχύτητας του σώματος σε συνάρτηση με το χρόνο για το χρονικό διάστημα \(0 s - 30 s\) φαίνεται στο διπλανό διάγραμμα.

4.1 Να υπολογίσετε τη μετατόπιση του σώματος κατά το χρονικό διάστημα \(0 s - 30 s\).
Μονάδες 6
4.2 Να σχεδιάσετε σε βαθμολογημένους άξονες το διάγραμμα επιτάχυνσης - χρόνου (α-t) για το χρονικό διάστημα \(0 s - 30 s\).
Μονάδες 6
4.3 Να συμπληρώσετε τον πίνακα:

Μονάδες 6
4.4 Να υπολογίσετε το έργο της συνισταμένης οριζόντιας δύναμης κατά τα τρία χρονικά διαστήματα: \(0\ s -10\ s\), \(10\ s -20\ s\) και \(20\ s -30\ s\). Σε ποιο χρονικό διάστημα προσφέρεται ενέργεια στο σώμα και σε ποιο χρονικό διάστημα αφαιρείται ενέργεια από το σώμα; Με ποιο γνωστό θεώρημα είναι συμβατά τα αποτελέσματά σας;
Μονάδες 7
Απάντηση Θέματος:
Ενδεικτική Λύση
4.1 To εμβαδόν που περικλείεται μεταξύ της γραφικής παράστασης της ταχύτητας και του άξονα των χρόνων είναι ίσο με την αλγεβρική τιμή της μετατόπισης, επομένως:
- Χρονικό διάστημα \(0\ s - 10\ s\):
$$Δ𝑥_1=\frac{(+40)\cdot10}{2}\ m=+200\ m$$
- Χρονικό διάστημα \(10\ s - 20\ s\):
$$Δ𝑥_2=(+40)\cdot10\ m=+400\ m$$
- Χρονικό διάστημα \(20\ s - 30\ s\):
$$Δ𝑥_3=\frac{(+40)\cdot10}{2}\ m=+200\ m$$
(Μονάδες 4)
- Η συνολική μετατόπιση είναι:
$$Δ𝑥 =Δ𝑥_1+Δ𝑥_2+Δ𝑥_3 \Rightarrow Δ𝑥 =+800\ m$$
(Μονάδες 2)
Εναλλακτικά, η συνολική μετατόπιση θα μπορούσε να βρεθεί και από το εμβαδό του τραπεζίου:
$$Δ𝑥 =\frac{10+30}{2}\cdot(+40)\ m=+800\ m$$
4.2 Η κλίση της ευθείας στο διάγραμμα της ταχύτητας σε συνάρτηση με το χρόνο, δίνει την αλγεβρική τιμή της επιτάχυνσης, οπότε:
- Χρονικό διάστημα \(0\ s - 10\ s\):
$$𝛼_1=\frac{Δ𝜐_1}{Δ𝑡_1} \Rightarrow 𝛼_1=\frac{+40 \frac{m}{s}}{10 s}\Rightarrow 𝛼_1=+4\frac{m}{s^2}$$
- Χρονικό διάστημα \(10\ s - 20\ s\):
$$𝛼_2=0 \frac{m}{s^2}$$
- Χρονικό διάστημα \(20\ s - 30\ s\):
$$𝛼_3=\frac{Δ𝜐_2}{Δ𝑡_2} \Rightarrow 𝛼_3=\frac{−40 \frac{m}{s}}{10 s} \Rightarrow 𝛼_3=−4\frac{m}{s^2}$$
(Μονάδες 3)
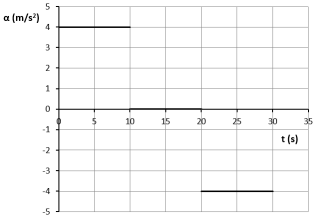
(Μονάδες 3)
4.3 Από 2ο νόμο του Νεύτωνα έχουμε \(𝛴𝐹 =𝑚𝑎\)

(Μονάδες 6)
4.4 Για το έργο της συνισταμένης δύναμης έχουμε:
- Χρονικό διάστημα \(0\ s - 10\ s\):
$$𝑊𝛴𝐹_1=𝛴𝐹_1\cdot Δ𝑥_1=(+40)\cdot(+200) J=+8.000\ J$$
- Χρονικό διάστημα \(10\ s - 20\ s\):
$$𝑊𝛴𝐹_2=𝛴𝐹_2\cdotΔ𝑥_2=0\cdot(+400)\ J=0\ J$$
- Χρονικό διάστημα \(20\ s - 30\ s\):
$$𝑊𝛴𝐹_3=𝛴𝐹_3\cdotΔ𝑥_3=(−40)\cdot(+200)\ J=−8.000\ J$$
(Μονάδες 2)
Στο χρονικό διάστημα \(0\ s - 10\ s\) προσφέρεται ενέργεια στο σώμα, αφού το έργο της συνισταμένης δύναμης είναι θετικό, ενώ στο χρονικό διάστημα \(20\ s - 30\ s\) αφαιρείται ενέργεια από το σώμα, αφού το έργο της συνισταμένης δύναμης είναι αρνητικό.
(Μονάδες 2)
Παρατηρούμε ότι το συνολικό έργο για τo χρονικό διάστημα από \(0\ s - 30\ s\) είναι:
$$𝑊=𝑊_{𝛴𝐹_1}+𝑊_{𝛴𝐹_2}+𝑊_{𝛴𝐹_3} \Rightarrow 𝑊=0\ J$$
Το αποτέλεσμα αυτό προκύπτει και με την εφαρμογή του θεωρήματος μεταβολής της κινητικής ενέργειας για τη συνολική μετατόπιση του σώματος:
$$𝛫_{𝜏𝜀𝜆}−𝛫_{𝛼𝜌𝜒}=𝑊$$
Αλλά \(𝛫_{𝜏𝜀𝜆}=𝛫_{𝛼𝜌𝜒}=0\ J\). Επομένως \(𝑊=0\ J\)
(Μονάδες 3)
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida).