Τράπεζα Θεμάτων

www.trapeza-thematon.gr

Τύπος Σχολείου:	Γενικό Λύκειο	Τάξη:	Β' Λυκείου
Μάθημα:	Φυσική Προσανατολισμού	Θέμα:	4
Κωδικός Θέματος:	16043	Ύλη:	1.1 Οριζόντια βολή 2.5 Η αρχή διατήρησης της ορμής 2.6 Μεγέθη που δε διατηρούνται στην κρούση

Τύπος Σχολείου:	Γενικό Λύκειο
Τάξη:	Β' Λυκείου
Μάθημα:	Φυσική Προσανατολισμού
Θέμα:	4
Κωδικός Θέματος:	16043
Ύλη:	1.1 Οριζόντια βολή 2.5 Η αρχή διατήρησης της ορμής 2.6 Μεγέθη που δε διατηρούνται στην κρούση
Τελευταία Ενημέρωση: 25-Αυγ-2022

ΘΕΜΑ 4

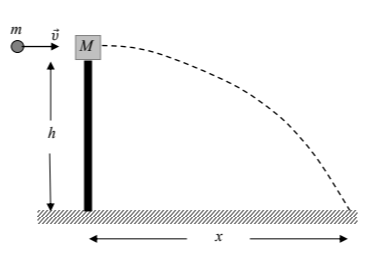
Ο καθηγητής Φυσικής σε μία σχολή αξιωματικών του στρατού θέτει ένα πρόβλημα σχετικά με το πώς οι φοιτητές, αξιοποιώντας τις γνώσεις τους από το μάθημα, θα μπορούσαν να υπολογίσουν την ταχύτητα $\vec{u}$ του βλήματος ενός πιστολιού. Ο καθηγητής υποδεικνύει στους φοιτητές την παρακάτω διαδικασία:
Το βλήμα μάζας $𝑚$ εκτοξεύεται οριζόντια και σφηνώνεται σε ένα κομμάτι ξύλου, μάζας 𝑀, που ισορροπεί ελεύθερο στην κορυφή ενός στύλου ύψους $ℎ$. Οι μάζες $𝑚$ και $𝑀$ μετρώνται με ζύγιση και το ύψος $ℎ$ μετράται με μετροταινία.
Το συσσωμάτωμα αμέσως μετά την κρούση εκτελεί οριζόντια βολή και χτυπάει στο έδαφος σε οριζόντια απόσταση $𝑥$ από τη βάση του στύλου, αφήνοντας ένα σημάδι στο χώμα ώστε να είναι δυνατή η μέτρηση αυτής της απόστασης $𝑥$.
Οι φοιτητές ακολούθησαν τη διαδικασία και έλαβαν μετρήσεις ακολουθώντας τη διαδικασία που τους υπέδειξε ο καθηγητής τους και κατέγραψαν τις τιμές:
$𝑚=0,1\ 𝑘𝑔$,
$𝑀=1,9\ 𝑘𝑔$,
$ℎ = 5\ 𝑚$ και
$𝑥 = 10\ 𝑚$.
Λαμβάνοντας υπόψη τις προηγούμενες τιμές των μεγεθών που μετρήθηκαν από τους φοιτητές, και θεωρώντας την αντίσταση του αέρα αμελητέα, να υπολογίσετε:

4.1. Το χρονικό διάστημα που πέρασε από την στιγμή της κρούσης μέχρι το συσσωμάτωμα να αγγίξει το έδαφος.
Μονάδες 6

4.2. Το μέτρο της οριζόντιας ταχύτητας $\vec{V}$ την οποία απέκτησε το συσσωμάτωμα αμέσως μετά την κρούση.
Μονάδες 6

4.3. Το μέτρο της ταχύτητας 𝜐⃗ του βλήματος πριν σφηνωθεί στο ξύλο.
Μονάδες 6

4.4. Την απώλεια της μηχανικής ενέργειας του συστήματος βλήμα-ξύλο κατά την κρούση.
Μονάδες 7

Δίνεται η επιτάχυνση της βαρύτητας στην επιφάνεια της Γης $𝑔 = 10\ 𝑚/𝑠^{2}$

Απάντηση Θέματος:

ΘΕΜΑ 4

4.1.

Το συσσωμάτωμα εκτελεί οριζόντια βολή.
Σύμφωνα με την αρχή ανεξαρτησίας των κινήσεων η κίνηση του προκύπτει από την επαλληλία της ελεύθερης πτώσης στον κατακόρυφο άξονα και της ευθύγραμμης ομαλής στον οριζόντιο.
Το χρονικό διάστημα που πέρασε από την στιγμή της κρούσης μέχρι το συσσωμάτωμα να αγγίξει το έδαφος $𝑡_{𝜋}$ υπολογίζεται από την εξίσωση κίνησης της ελεύθερης πτώσης για ύψος $ℎ = 5 𝑚:$

$$\begin{align} ℎ=\dfrac{1}{2}\cdot 𝑔\cdot 𝑡_{𝜋}^{2}\\ \Rightarrow 𝑡_{𝜋} =\sqrt{\dfrac{2\cdot ℎ}{𝑔}}\\ \Rightarrow 𝑡_{𝜋}=1\ 𝑠\end{align}$$

Μονάδες 6

4.2. Κατά την οριζόντια βολή η τροχιά είναι παραβολική και η εξίσωση της προκύπτει από τις εξισώσεις κίνησης της ευθύγραμμης ομαλής κίνησης και της ελεύθερης πτώσης με απαλοιφή του χρόνου:

Οριζόντιος άξονας:

$$𝑥=𝑉\cdot 𝑡$$ $$\Rightarrow 𝑡=\dfrac{𝑥}{𝑉}$$

Κατακόρυφος άξονας:

$$𝑦=\dfrac{1}{2}\cdot 𝑔\cdot 𝑡^{2}$$ $$\Rightarrow 𝑦=\dfrac{1}{2}\cdot 𝑔\cdot \dfrac{x^{2}}{V^{2}}$$

Το μέτρο της οριζόντιας ταχύτητας $𝑉$ την οποία απέκτησε το συσσωμάτωμα αμέσως μετά την κρούση υπολογίζεται θέτοντας στην εξίσωση της παραβολής $𝑦 = 5\ 𝑚$ και $𝑥 = 10\ 𝑚$ οπότε:

$$𝑉=\sqrt{\dfrac{𝑔\cdot 𝑥^2}{2\cdot 𝑦}}$$ $$\Rightarrow V=10\ 𝑚/𝑠$$

Εναλλακτικά:

$$𝑥=𝑉\cdot 𝑡_{𝜋}$$ $$\Rightarrow 𝑉=\dfrac{𝑥}{𝑡_{𝜋}}$$ $$\Rightarrow 𝑉=10\ 𝑚/𝑠$$

Μονάδες 6

4.3. Στον άξονα που πραγματοποιείται η κρούση το σύστημα βλήμα-ξύλο δεν δέχεται εξωτερικές δυνάμεις, οπότε είναι μονωμένο και η ορμή του διατηρείται:

$$\vec{p}_{πριν}=\vec{p}_{μετά}$$

Λαμβάνοντας ως θετική τη φορά της ταχύτητας του βλήματος πριν την κρούση:

$$𝑚\cdot 𝜐=(𝑚+𝑀)\cdot 𝑉$$ $$\Rightarrow 0,1\cdot 𝜐\ 𝑘𝑔\cdot \dfrac{𝑚}{𝑠}=2\ 𝑘𝑔\cdot 10\ 𝑚/𝑠$$ $$\Rightarrow 𝜐=200\ 𝑚/𝑠$$

Μονάδες 6

4.4. Επειδή το βλήμα και το ξύλο θεωρούνται υλικά σημεία πρακτικά ακριβώς πριν και ακριβώς μετά την κρούση βρίσκονται στην ίδια θέση οπότε η δυναμική ενέργεια δεν αλλάζει και έτσι η απώλεια της μηχανικής ενέργειας κατά την πλαστική κρούση θα είναι ίση με την μείωση της κινητικής ενέργειας του συστήματος:

$$𝛦_{𝛼𝜋𝜔𝜆}=\dfrac{1}{2}\cdot 𝑚\cdot 𝜐^{2}-\dfrac{1}{2}\cdot (𝑚+𝑀)𝑉^{2}$$ $$\Rightarrow 𝛦_{𝛼𝜋𝜔𝜆}=1900\ 𝐽$$

Μονάδες 7

Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida).