Τράπεζα Θεμάτων

www.trapeza-thematon.gr

Τύπος Σχολείου:	Γενικό Λύκειο	Τάξη:	Β' Λυκείου
Μάθημα:	Μαθηματικά Προσανατολισμού	Θέμα:	4
Κωδικός Θέματος:	22273	Ύλη:	2.2. Γενική Μορφή Εξίσωσης Ευθείας

Τύπος Σχολείου:	Γενικό Λύκειο
Τάξη:	Β' Λυκείου
Μάθημα:	Μαθηματικά Προσανατολισμού
Θέμα:	4
Κωδικός Θέματος:	22273
Ύλη:	2.2. Γενική Μορφή Εξίσωσης Ευθείας
Τελευταία Ενημέρωση: 09-Μαΐ-2023

ΘΕΜΑ 4

Δίνεται η έλλειψη με εξίσωση:

$\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1 (1)$

α) Να προσδιορίσετε, δικαιολογώντας την απάντησή σας, τις συντεταγμένες:
i. των σημείων που η έλλειψη τέμνει τους άξονες $x^{'} x$ και $y^{'} y$ ,
ii. των εστιών $Ε$ και $Ε^{'}$ της έλλειψης.
(Μονάδες 12)

β) Να βρείτε τις εξισώσεις των ευθειών που διέρχονται από το σημείο $Α (0, 4)$ και εφάπτονται στη καμπύλη που περιγράφει η εξίσωση $(1)$ .
(Μονάδες 13)

Απάντηση Θέματος:

α) Η εξίσωση $(1)$ είναι της μορφής $\frac{x^{2}}{α^{2}} + \frac{y^{2}}{β^{2}} = 1$ , όπου $α^{2} = 9$ και $β^{2} = 4$ .
i. Για να βρούμε τα σημεία τομής της έλλειψης αυτής με τον άξονα $x^{'} x$ θέτουμε στην εξίσωση $(1)$ $y = 0$ . Έτσι έχουμε

$\frac{x^{2}}{9} = 1$ $⟺ x^{2} = 9$ $⟺ x = \pm 3.$

Τα σημεία τομής με τον άξονα $x^{'} x$ είναι, λοιπόν, τα σημεία $Κ (3, 0)$ και $Κ^{'} (- 3, 0)$ . Αντίστοιχα, για να βρούμε τα σημεία τομής της έλλειψης αυτής με τον άξονα $y^{'} y$ θέτουμε στην εξίσωση $(1)$ $x = 0$ . Έτσι έχουμε

$\frac{y^{2}}{4} = 1$ $⟺ y^{2} = 4$ $⟺ y = \pm 2.$

Επομένως, τα σημεία τομής με τον άξονα $y^{'} y$ είναι τα σημεία $B (0, 2)$ και $Β^{'} (0, - 2)$ .
ii. Η εξίσωση $(1)$ παριστάνει έλλειψη με εστίες στον άξονα $x^{'} x$ . Οπότε οι εστίες έχουν συντεταγμένες $Ε (γ, 0)$ και $Ε^{'} (- γ, 0)$ , όπου $γ = \sqrt{α^{2} - β^{2}} = \sqrt{5}$ . Άρα οι εστίες της, $Ε$ και $Ε^{'}$ , έχουν συντεταγμένες $Ε (\sqrt{5}, 0)$ και $Ε^{'} (- \sqrt{5}, 0) .$

β)

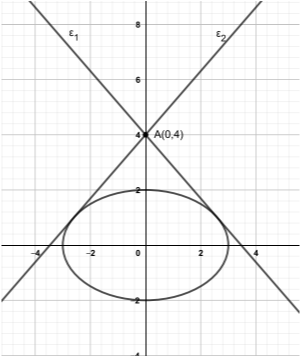
Το σημείο $Α (0, 4)$ είναι εξωτερικό σημείο της έλλειψης, αφού είναι σημείο στον άξονα $y^{'} y$ και η έλλειψη που μας δόθηκε τέμνει τον άξονα $y^{'} y$ στα σημεία $Β (0, 2)$ και $Β^{'} (0, - 2)$ . Θεωρούμε $Μ (x_{1}, y_{1})$ το σημείο επαφής. Η εξίσωση της εφαπτόμενης $(ε)$ στο σημείο $Μ$ θα είναι της μορφής

$\frac{x x_{1}}{9} + \frac{y y_{1}}{4} = 1 ⟺ 4 x x_{1} + 9 y y_{1} = 36.$

Η ευθεία $(ε)$ διέρχεται από το σημείο $Α (0, 4)$ , οπότε οι συντεταγμένες του σημείου $Α$ επαληθεύουν την εξίσωση της ευθείας $(ε)$ . Ισχύει δηλαδή

$4 \cdot 0 x_{1} + 9 \cdot 4 y_{1} = 36 ⟺ y_{1} = 1.$

Επιπλέον, το σημείο $Μ (x_{1}, y_{1})$ είναι σημείο της έλλειψης, οπότε οι συντεταγμένες του ικανοποιούν την εξίσωση $(1)$ . Άρα ισχύει

$\begin{aligned} \frac{x_{1}^{2}}{9} + \frac{y_{1}^{2}}{4} = 1 \\ ⟺ & \frac{x_{1}^{2}}{9} + \frac{1^{2}}{4} = 1 \\ ⟺ & \frac{x_{1}^{2}}{9} = \frac{3}{4} \\ ⟺ & x_{1} = \pm \frac{3 \sqrt{3}}{2} . \end{aligned}$

Για $x_{1} = \frac{3 \sqrt{3}}{2}$ και $y_{1} = 1$ , έχουμε την εφαπτόμενη $(ε_{1})$ με εξίσωση

$4 \frac{3 \sqrt{3}}{2} x + 9 y = 36 ⟺ 2 \sqrt{3} + 3 y = 12.$

Για $x_{1} = - \frac{3 \sqrt{3}}{2}$ και $y_{1} = 1$ , έχουμε την εφαπτόμενη $(ε_{2})$ με εξίσωση

$4 (- \frac{3 \sqrt{3}}{2}) x + 9 y = 36 ⟺ - 2 \sqrt{3} x + 3 y = 12.$

Άρα, οι δύο εφαπτόμενες της έλλειψης που διέρχονται από το σημείο $Α (0, 4)$ είναι οι:

$2 \sqrt{3} + 3 y = 12$ $και - 2 \sqrt{3} x + 3 y = 12$

Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida).