Τράπεζα Θεμάτων

www.trapeza-thematon.gr

Τύπος Σχολείου:	Γενικό Λύκειο	Τάξη:	Α' Λυκείου
Μάθημα:	Φυσική	Θέμα:	2
Κωδικός Θέματος:	8000	Ύλη:	Χωρίς Αντιστοίχιση Ύλης

Τύπος Σχολείου:	Γενικό Λύκειο
Τάξη:	Α' Λυκείου
Μάθημα:	Φυσική
Θέμα:	2
Κωδικός Θέματος:	8000
Ύλη:	Χωρίς Αντιστοίχιση Ύλης
Τελευταία Ενημέρωση: 29-Απρ-2024

ΘΕΜΑ Β

Β1) Σε ένα κιβώτιο που αρχικά ήταν ακίνητο πάνω σε λείο οριζόντιο επίπεδο, ασκείται οριζόντια δύναμη $\vec{F}$ . Το κιβώτιο κινείται πάνω στο οριζόντιο επίπεδο με ταχύτητα που αυξάνεται ανάλογα με το χρόνο.

Α) Να επιλέξετε την σωστή απάντηση.
Η γραφική παράσταση της τιμής της δύναμης $(F)$ που ασκείται στο κιβώτιο σε συνάρτηση με το χρόνο $(t)$ παριστάνεται σωστά από το διάγραμμα:

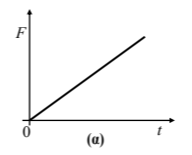
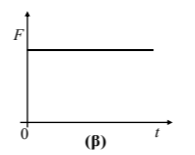
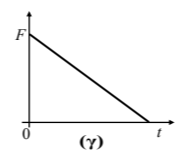
Μονάδες 4

Β) Να δικαιολογήσετε την επιλογή σας.
Μονάδες 8

B2) Μικρό σφαιρίδιο μάζας $m$ αφήνεται τη χρονική στιγμή $t = 0 s$ από μικρό ύψος $h$ να εκτελέσει ελεύθερη πτώση. Έστω $t_{ο λ ι κ ο}$ το χρονικό διάστημα που απαιτείται για να φτάσει το σφαιρίδιο στο έδαφος και $t_{Ε}$ το χρονικό διάστημα που απαιτείται ώστε η δυναμική του ενέργεια να γίνει ίση με την κινητική του.
Ως επίπεδο αναφοράς για τη δυναμική ενέργεια θεωρείται το οριζόντιο έδαφος και η επίδραση του αέρα αμελητέα.

Α) Να επιλέξετε την σωστή απάντηση.

Ο λόγος ισούται με:

α) $\sqrt{2}$
β) $\frac{3}{2}$
γ) $2$
Μονάδες 4

Β) Να δικαιολογήσετε την επιλογή σας.
Μονάδες 9

Απάντηση Θέματος:

Β1. Σωστή απάντηση είναι η (β)
Ενδεικτική Αιτιολόγηση
Εφόσον η ταχύτητα αυξάνεται ανάλογα με το χρόνο, το κιβώτιο θα επιταχύνεται με σταθερή επιτάχυνση.
Από τον 2ο Νόμο του Νεύτωνα, αφού η τιμή της επιτάχυνσης είναι σταθερή, θα είναι και η τιμή της δύναμης σταθερή. Άρα το διάγραμμα της τιμής της δύναμης σε συνάρτηση με το χρόνο θα είναι μία ευθεία παράλληλη στον άξονα του χρόνου.

Β2. Σωστή απάντηση είναι η (α).

Ενδεικτική Αιτιολόγηση
Σύμφωνα με τις εξισώσεις της ελεύθερης πτώσης:

$h = \frac{1}{2} \cdot g \cdot t_{ο λ ι κ ό}^{2}$

από όπου προκύπτει ότι:

$t_{ο λ ι κ ο} = \sqrt{\frac{2 h}{g}}$

Στο ύψος $h$ το σφαιρίδιο έχει δυναμική ενέργεια :
$U = m \cdot g \cdot h$ κινητική ενέργεια $Κ = 0$ και μηχανική ενέργεια:

$Ε = U + Κ = m \cdot g \cdot h$

Έστω ότι σε ύψος $h^{'}$ από το έδαφος η δυναμική ενέργεια του σφαιριδίου έχει γίνει ίση με την κινητική του.

H δυναμική του ενέργεια θα είναι : $U^{'} = m \cdot g \cdot h^{'}$ ,
η κινητική του ενέργεια : $Κ^{'} = U^{'}$
και η μηχανική ενέργεια: $Ε^{'} = Κ^{'} + U^{'} = 2 U^{'} = 2 m \cdot g \cdot h^{'}$ .

Από την αρχή διατήρησης της μηχανικής ενέργειας προκύπτει :

$Ε^{'} = Ε$ $2 m \cdot g \cdot h^{'} = m \cdot g \cdot h$

και τελικά

$h^{'} = \frac{h}{2}$

Το σφαιρίδιο κατά την πτώση του από το ύψος $h$ σε ύψος $h^{'}$ , διανύει απόσταση $s = h - h^{'} = \frac{h}{2}$

Όπως παραπάνω βρίσκουμε ότι:

$t_{E} = \sqrt{\frac{2 s}{g}} = \sqrt{\frac{h}{g}}$

Οπότε:

$\frac{t_{ο λ ι κ ό}}{t_{E}} = \sqrt{2}$

Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida).