Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 6895 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 11702 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 24-Νοε-2021 | Ύλη: | Χωρίς Αντιστοίχιση Ύλης | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Φυσική | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 11702 | ||
| Ύλη: | Χωρίς Αντιστοίχιση Ύλης | ||
| Τελευταία Ενημέρωση: 24-Νοε-2021 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ Δ
Ένα σώμα μάζας \(20 Kg\) κινείται πάνω σε λείο οριζόντιο επίπεδο. Το διάγραμμα της ταχύτητας του σώματος σε συνάρτηση με το χρόνο για το χρονικό διάστημα \(0 s- 30 s\) φαίνεται στο σχήμα.

Δ1) Να υπολογιστεί η συνολική μετατόπιση του σώματος στο χρονικό διάστημα \(0 s - 30 s\).
Μονάδες 6
Δ2) Να συμπληρωθεί ο πίνακας:
| Χρονικό διάστημα (s) | Συνισταμένη οριζόντια δύναμη που ασκείται στο σώμα (Ν) |
|---|---|
| 0-10 | |
| 10-30 |
Μονάδες 6
Δ3) Να υπολογιστεί το έργο της συνισταμένης οριζόντιας δύναμης τα χρονικά διαστήματα \(0 s - 10 s\), και \(10 s - 30 s\).
Μονάδες 6
Δ4) Με βάση τα αποτελέσματα του ερωτήματος \((Δ3)\) να επαληθεύσετε το «Θεώρημα Μεταβολής της Κινητικής Ενέργειας - Έργου».
Μονάδες 7
Ενδεικτική Λύση
Δ1) Η συνολική μετατόπιση του σώματος στο χρονικό διάστημα \(0 s - 30 s\) υπολογίζεται από το εμβαδόν του διαγράμματος:
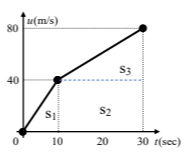
\(S_{ολ}=S_1+S_2+S_3\Rightarrow S_{ολ}=\dfrac{1}{2}40\cdot 10+\dfrac{40+80}{2}\cdot 20\Rightarrow S_{ολ}=1400m\)
Δ2) Οι τιμές του πίνακα υπολογίζονται από τις σχέσεις:
$$α_1 =\dfrac{Δυ}{Δt}\Rightarrow α_1=\dfrac{40-0m}{10-0s^2}\Rightarrow α_1=4\dfrac{m}{s^2}$$
$$F_1 = m\cdot α_1\Rightarrow F_1 = 20\cdot 4 Ν\Rightarrow F_1 = 80 Ν$$
$$α_2=\dfrac{Δυ}{Δt}\Rightarrow α_2=\dfrac{80-40m}{30-10s^2}\Rightarrow α_2=2\dfrac{m}{s^2}$$
$$F_2 = m\cdot α_2\Rightarrow F_2 = 20\cdot 2 Ν\Rightarrow F_2 = 40 Ν$$
| Χρονικό διάστημα (s) | Συνισταμένη οριζόντια δύναμη που ασκείται στο σώμα (Ν) |
|---|---|
| 0-10 | 80 |
| 10-30 | 40 |
Δ3) Το έργο υπολογίζεται:
$$W_{{0s}-{10s}}=F_1\cdot x_{{0s}-{10s}}$$
όπου$$x_{0s-10s}=\dfrac{1}{2}α_1\cdot (0-10)^2 \ (SI)$$
$$x_{0s-10s}=200m$$
\(W_{10s - 30s} = F_1 x_{10-30}\), όπου
$$x_{10s-30s}=x_0+\dfrac{1}{2}α_2(30-10)^2$$ $$\Rightarrow x_{10s-30s}=υ_0Δt+\dfrac{1}{2}α_2\cdot {20}^2 \ (SI)$$
Όπου
\(υ_0=40\dfrac{m}{s}\) από το διάγραμμα \(υ - t\).
$$x_{0s-10s}=x_0+\dfrac{1}{2}α_2\cdot (30-10)^2 \ (SI)$$ $$x_{0s-10s}=40\cdot 20+\dfrac{1}{2}40\cdot {20}^2m$$ $$\Rightarrow x_{0s-10s}=1200m$$
άρα
$$W_{0s - 10s} = 80\cdot 200J\Rightarrow W_{0s - 10s} = 16000 J$$
$$W_{10s - 30s} = 40\cdot 1200J\Rightarrow W_{10s - 30s} = 48000J$$
Δ4) Για το Θεώρημα Μεταβολής της Κινητικής Ενέργειας - Έργου (Θ.Μ.Κ.Ε.) ισχύει:
$$Κ_{τελ}- Κ_{αρχ} = W_{ολ}$$ $$Κ_{τελ} - 0 = W_{ολ}$$
όπου από τη (Δ2)
$$W_{ολ} = W_{0s - 10s} + W_{10s - 30s}\Rightarrow W_{ολ}= 1600J + 48000J\Rightarrow W_{ολ} = 64000 J$$
και
$$Κ_{τελ}=\dfrac{1}{2}m\cdot υ^2_{τελ.}$$
όπου \(υ_{τελ.}=80\dfrac{m}{s}\) όπως δίνεται από το διάγραμμα \(υ - t\).
$$Κ_{τελ} = 64000 J$$
άρα ισχύει το Θ.Μ.Κ.Ε.