Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 11307 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 13269 | Θέμα: | 2 | |
| Τελευταία Ενημέρωση: | 21-Φεβ-2024 | Ύλη: | 1.1.9. Οι εξισώσεις προσδιορισμού της ταχύτητας και της θέσης ενός κινητού στην ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 1.2.3 Ο πρώτος νόμος του Νεύτωνα 1.3.1 Τρίτος νόμος του Νεύτωνα. Νόμος Δράσης - Αντίδρασης | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Φυσική | ||
| Θέμα: | 2 | ||
| Κωδικός Θέματος: | 13269 | ||
| Ύλη: | 1.1.9. Οι εξισώσεις προσδιορισμού της ταχύτητας και της θέσης ενός κινητού στην ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 1.2.3 Ο πρώτος νόμος του Νεύτωνα 1.3.1 Τρίτος νόμος του Νεύτωνα. Νόμος Δράσης - Αντίδρασης | ||
| Τελευταία Ενημέρωση: 21-Φεβ-2024 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 2
2.1 Σημειακό αντικείμενο κινείται ευθύγραμμα και σε δύο οποιαδήποτε, ίσα μεταξύ τους, χρονικά διαστήματα \(Δt\) διανύει ίσα διαστήματα \(S\).
Α. Το παραπάνω δεδομένο μπορεί να μας οδηγήσει στο συμπέρασμα ότι η κίνηση του σημειακού αντικειμένου είναι ευθύγραμμη ομαλή;
α) ΝΑΙ
β) ΟΧΙ
Μονάδες 4
Β. Να δικαιολογήσετε την απάντησή σας.
Μονάδες 8
2.2 Σημειακό αντικείμενο αφήνεται ελεύθερο από ύψος \(h\) πάνω από την επιφάνεια της Γης, τη χρονική στιγμή \(t_{0}= 0\).
Α. Αν αμελήσουμε τις δυνάμεις που το σημειακό αντικείμενο δέχεται από τον ατμοσφαιρικό αέρα και αν θεωρήσουμε τη βαρυτική επιτάχυνση \(\vec{g}\) σταθερή, τότε, την τυχαία χρονική στιγμή \(t\), η γήινη βαρυτική δυναμική ενέργεια του κινητού υπολογίζεται από τη σχέση:
α) \(U = m \cdot g \cdot h\)
β) \(U = m \cdot g \cdot (\dfrac{1}{2}\cdot g \cdot t^{2})\)
γ) \(U =m \cdot g \cdot (h -\dfrac{1}{2}\cdot g \cdot t^{2})\)
Μονάδες 4
Β. Να δικαιολογήσετε την απάντησή σας.
Μονάδες 9
ΘΕΜΑ 2
2.1
Α. β)
Μονάδες 4
Β. Στην ευθύγραμμη ομαλή κίνηση, το σημειακό κινητό σε δύο οποιαδήποτε, ίσα μεταξύ τους, χρονικά διαστήματα \(Δt\) μετατοπίζεται εξίσου κατά \(Δx\) (η φορά της κίνησης του κινητού δεν μεταβάλλεται). Τα ίσα διαστήματα \(S\) μπορούν να διανύονται με αντίθετες φορές κίνησης και σ’ αυτήν την περίπτωση η κίνηση ΔΕΝ είναι ευθύγραμμη ομαλή.
Μονάδες 8
2.2
Α. γ)
Μονάδες 4
Β.
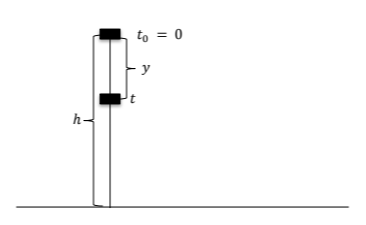
Το σημειακό αντικείμενο εκτελεί ελεύθερη πτώση, χωρίς αρχική ταχύτητα. Έτσι, τη χρονική στιγμή \(t\) το σημειακό αντικείμενο έχει μετατοπιστεί κατά \(y =\dfrac{1}{2}\cdot g \cdot t^{2}\), οπότε η γήινη βαρυτική δυναμική ενέργειά του είναι:
$$U = m \cdot g \cdot (h - y)$$ $$=m \cdot g \cdot (h -\dfrac{1}{2}\cdot g \cdot t^{2})$$
Μονάδες 9
