Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 13779 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 13467 | Θέμα: | 2 | |
| Τελευταία Ενημέρωση: | 26-Φεβ-2024 | Ύλη: | 1.1 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ 2.1.2 Έργο βάρους και μεταβολή της κινητικής ενέργειας | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Φυσική | ||
| Θέμα: | 2 | ||
| Κωδικός Θέματος: | 13467 | ||
| Ύλη: | 1.1 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ 2.1.2 Έργο βάρους και μεταβολή της κινητικής ενέργειας | ||
| Τελευταία Ενημέρωση: 26-Φεβ-2024 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ2
Β1.
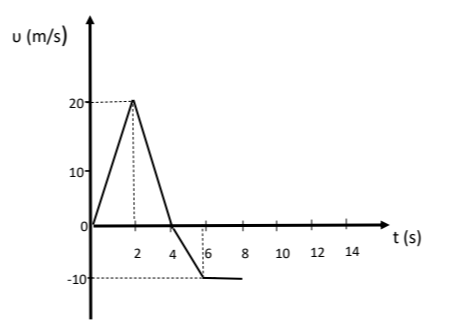
Κινητό, του οποίου το διάγραμμα ταχύτητας - χρόνου είναι το παραπάνω, αρχίζει να κινείται την χρονική στιγμή \(t=0\ s\) κατά την θετική φορά του άξονα \(xx'\).
Α. Να επιλέξετε την σωστή απάντηση.
(Μονάδες 4)
α. Το κινητό επιστρέφει για πρώτη φορά στη θέση από την οποία ξεκίνησε την χρονική στιγμή \(t=4\ s\).
β. Το κινητό επιστρέφει για πρώτη φορά στη θέση από την οποία ξεκίνησε την χρονική στιγμή \(t=8\ s\).
γ. Το κινητό επιστρέφει για πρώτη φορά στη θέση από την οποία ξεκίνησε μετά την χρονική στιγμή \(t=8\ s\).
Β. Να δικαιολογήσετε την επιλογή σας.
(Μονάδες 8)
Β2.
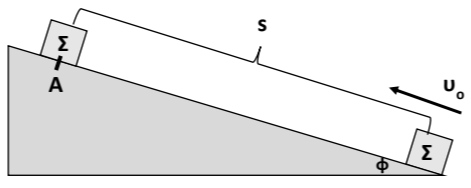
Το σώμα \(Σ\) του σχήματος, εκτοξεύεται με αρχική ταχύτητα μέτρου \(υ_{0}\) από την βάση του κεκλιμένου επιπέδου, το οποίο δεν είναι λείο. Στην θέση \(Α\) και αφού διανύσει διάστημα \(s\) επάνω στο κεκλιμένο επίπεδο, η ταχύτητά του μηδενίζεται στιγμιαία και στη συνέχεια επιστρέφει στο σημείο από το οποίο ξεκίνησε περνώντας από αυτό με ταχύτητα μέτρου \(υ\).
Α. Να επιλέξετε την σωστή απάντηση.
(Μονάδες 4)
α. \(υ_{0}>υ\)
β. \(υ_{0}<υ\)
γ. \(υ_{0}=υ\)
Β. Να δικαιολογήσετε την επιλογή σας.
(Μονάδες 9)
B1.
Α. Σωστή η απάντηση (γ).
Β. Ενδεικτική Δικαιολόγηση
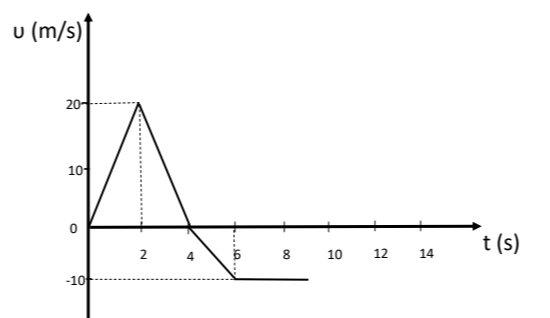
Από \(0\ s - 4\ s\) το κινητό κινείται κατά την θετική φορά του άξονα και συγκεκριμένα:
Από \(0\ s - 2\ s\) επιταχύνεται ομαλά ενώ από \(2\ s - 4\ s\) επιβραδύνεται ομαλά και την χρονική στιγμή \(4\ s\) η ταχύτητά του μηδενίζεται.
Από \(0\ s - 4\ s\) το διάστημα που διανύει υπολογίζεται από το εμβαδόν του τριγώνου (ως η απόλυτη τιμή της μετατόπισης):
$$s=\dfrac{4\ s\cdot 20\ \dfrac{m}{s}}{2}=40\ m$$
Από την χρονική στιγμή \(4\ s\) και μετά το κινητό κινείται κατά την αρνητική φορά του άξονα επιστρέφοντας προς το σημείο από το οποίο ξεκίνησε.
Το διάστημα που διανύει επιστρέφοντας και για το χρονικό διάστημα \(4\ s - 8\ s\) είναι (ως η απόλυτη τιμή της μετατόπισης):
$$s'=\dfrac{(4\ s+2\ s)\cdot 10\ \dfrac{m}{s}}{2}$$ $$=30\ m\ \ \text{(εμβαδόν τραπεζίου)}$$
Δηλ. την στιγμή \(8\ s\) βρίσκεται στην θέση \((40-30)\ m=10\ m\) και συνεχίζει να κινείται προς τα αριστερά.
Άρα επιστρέφει στο σημείο από το οποίο ξεκίνησε μετά την χρονική στιγμή \(8\ s\).
B2.
Α. Σωστή η απάντηση (α).
Β. Ενδεικτική Αιτιολόγηση
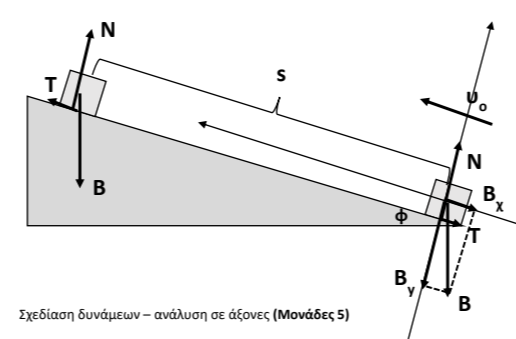
Το σώμα κινούμενο από την βάση του κεκλιμένου επιπέδου προς το σημείο όπου σταματά στιγμιαία και επιστρέφοντας ξανά στην βάση, διανύει μια κλειστή διαδρομή.
Εφαρμόζουμε το θεώρημα έργου ενέργειας:
$$W_{\text{βαρ}}=0$$
(Επειδή το βάρος είναι συντηρητική δύναμη)
$$ΣF_{y}=0 $$ $$\Rightarrow N=m \cdot g \cdot συνφ\ \ \ \ (1)$$
$$Τ=μΝ $$ $$\overset{(1)}{\Rightarrow} Τ=μ \cdot m \cdot g \cdot συνφ\ \ \ \ (2)$$
$$Κ_{\text{τελ}}-Κ_{\text{αρχ}}=W_{ολ} $$ $$\Rightarrow \dfrac{1}{2}mυ^{2}-\dfrac{1}{2}mυ_{0}^{2}=W_{\text{βαρ}}+W_{T}$$ $$\overset{(2)}{\Rightarrow} \dfrac{1}{2}mυ^{2}-\dfrac{1}{2}mυ_{0}^{2}=0-2 \cdot μ \cdot m \cdot g \cdot συνφ \cdot s $$ $$\Rightarrow υ=\sqrt{υ_{0}^{2}-2 \cdot μ \cdot g \cdot συνφ \cdot s} $$ $$\Rightarrow υ < υ_{0}$$
