Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 19359 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 13669 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 31-Μαΐ-2024 | Ύλη: | 1.1.5. Η έννοια της ταχύτητας στη ευθύγραμμη ομαλή κίνηση 1.3.4 Ανάλυση δύναμης σε συνιστώσες 1.3.7 Ο νόμος της τριβής 1.3.9 Ο δεύτερος νόμος του Νεύτωνα σε διανυσματική και σε αλγεβρική μορφή 2.1.1 Η έννοια του έργου 2.1.2 Έργο βάρους και μεταβολή της κινητικής ενέργειας | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Φυσική | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 13669 | ||
| Ύλη: | 1.1.5. Η έννοια της ταχύτητας στη ευθύγραμμη ομαλή κίνηση 1.3.4 Ανάλυση δύναμης σε συνιστώσες 1.3.7 Ο νόμος της τριβής 1.3.9 Ο δεύτερος νόμος του Νεύτωνα σε διανυσματική και σε αλγεβρική μορφή 2.1.1 Η έννοια του έργου 2.1.2 Έργο βάρους και μεταβολή της κινητικής ενέργειας | ||
| Τελευταία Ενημέρωση: 31-Μαΐ-2024 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Το σώμα του σχήματος, μάζας \(𝑚=1 Kg\), διέρχεται τη χρονική στιγμή \(𝑡_0=0 s\) από τη θέση Α του λείου οριζοντίου επιπέδου \(ΑΓ\) ( μήκους \(𝛢𝛤= 20\ m\)) με ταχύτητα μέτρου \(𝜐_0\). Τη χρονική στιγμή \(𝑡_1=2\ s\) το σώμα έχει φτάσει στη θέση \(Γ\) και, χωρίς να αναπηδήσει, συνεχίζει την κίνησή του, ολισθαίνοντας στο κεκλιμένο επίπεδο \(ΓΕ\) (μεγάλου μήκους), γωνίας κλίσης \(𝜑=30^0\), με το οποίο παρουσιάζει συντελεστή τριβής ολίσθησης \(μ_{ολ} =\dfrac{\sqrt3}{3}\).
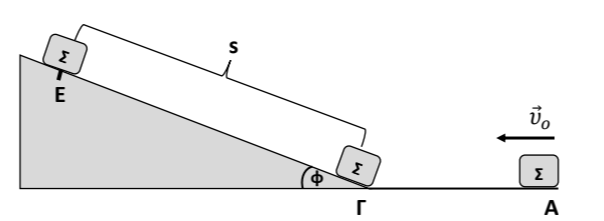
4.1 Να σχεδιάσετε τις δυνάμεις που ασκούνται στο σώμα, καθώς αυτό κινείται στο επίπεδο \(ΑΓ\) και να υπολογίσετε την κινητική του ενέργεια στη θέση \(Γ\).
Μονάδες 5
4.2 Να σχεδιάσετε τις δυνάμεις που ασκούνται στο σώμα σε μια θέση μεταξύ \(Γ\) και \(Ε\), καθώς αυτό ανεβαίνει και να τις αναλύσετε σε δύο κάθετους μεταξύ τους άξονες, εκ των οποίων ο ένας να είναι ο άξονας κίνησης.
Μονάδες 5
4.3 Να υπολογίσετε το διάστημα \(𝑠\) που θα διανύσει το σώμα στο κεκλιμένο επίπεδο μέχρι να μηδενιστεί η ταχύτητά του.
Μονάδες 8
4.4 Να σχεδιάσετε τις δυνάμεις που ασκούνται στο σώμα στη θέση \(Ε\), αφού έχει μηδενιστεί η ταχύτητά του.
Να διερευνήσετε αν θα επιστρέψει στη βάση του κεκλιμένου επιπέδου.
Να δικαιολογήσετε την απάντησή σας.
Να δεχθείτε ότι η μέγιστη στατική τριβή είναι ίση με την τριβή ολίσθησης.
Μονάδες 7
Δίνονται: \(𝜂𝜇30^0=\dfrac{1}{2}\), \(𝜎𝜐𝜈30^0=\dfrac{\sqrt{3}}{2}\), \(𝑔=10 \dfrac{m}{s^2}\)
Ενδεικτική λύση
4.1
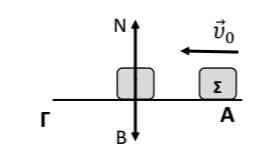
Σχεδίαση δυνάμεων:
(Μονάδες 2)
Το οριζόντιο επίπεδο \(ΑΓ\) είναι λείο, άρα δεν ασκείται δύναμη τριβής κατά μήκος του οριζόντιου άξονα \(x’x\).
Επίσης δεν ασκείται άλλη οριζόντια δύναμη στο σώμα, οπότε \(𝛴𝐹_𝑥=0\). Επίσης \(𝛴𝐹_𝑦=0\).
Άρα, το σώμα \(Σ\) εκτελεί στο επίπεδο αυτό Ευθύγραμμη Ομαλή Κίνηση: \(𝜐_𝛤=𝜐_𝛢=𝜐_0\),
$$𝛢𝛤=𝜐_0\cdot 𝑡\Rightarrow𝜐_0=\dfrac{𝛢𝛤}{𝑡}=\dfrac{20𝑚}{2𝑠}\Rightarrow υ_0=10\ m/s$$
Η Κινητική Ενέργεια του σώματος στο \(Γ\) είναι :
$$𝛫=\dfrac{1}{2}\cdot 𝑚\cdot 𝜐^2_𝛤=\dfrac{1}{2}\cdot 1 Kg\cdot (10\dfrac{m}{s})^2 \Rightarrow K=50\ J$$
(Μονάδες 3)
4.2
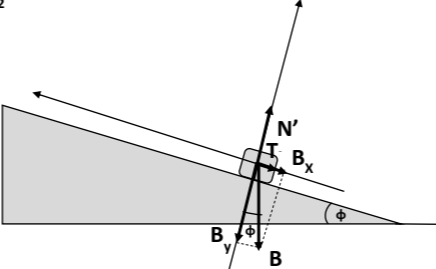
Σχεδίαση δυνάμεων κατά την άνοδο του σώματος-Ανάλυση σε άξονες:
(Μονάδες 5)
4.3
Από την ισορροπία στον άξονα \(y'y\) έχουμε:
$$𝛴𝐹_𝑦=0\Rightarrow𝑁'−𝑚\cdot 𝑔\cdot 𝜎𝜐𝜈30^0=0$$ $$\Rightarrow 𝛮'=𝑚\cdot 𝑔\cdot 𝜎𝜐𝜈30^0, (1)$$
(Μονάδα 1)
Οπότε:
$$𝑇_{𝑜𝜆}=𝜇\cdot 𝛮'$$ $$\overset{(1)}{\Rightarrow} 𝑇_{𝑜𝜆}=𝜇\cdot 𝑚\cdot 𝑔\cdot 𝜎𝜐𝜈30^0,\ (2)$$
(Μονάδα 1)
Εφαρμόζουμε το Θ.Μ.Κ.Ε. από τη βάση του κεκλιμένου επιπέδου έως την θέση όπου μηδενίζεται η ταχύτητα του σώματος.
$$𝛫_{𝜏𝜀𝜆}−𝛫_{𝛼𝜌𝜒}=𝑊_𝐵+𝑊_{𝛵𝜊𝜆}$$ $$\Rightarrow 0−\dfrac{1}{2}𝑚\cdot 𝜐^2_𝛤=−𝑚\cdot 𝑔\cdot 𝜂𝜇30^0\cdot 𝑠 −𝛵_{𝜊𝜆}\cdot 𝑠$$
(Μονάδες 3)
$$\overset{(2)}{\Rightarrow} 0−\dfrac{1}{2}𝑚\cdot 𝜐^2_𝛤= −𝑚\cdot 𝑔\cdot 𝜂𝜇30^0\cdot 𝑠−𝜇\cdot 𝑚\cdot 𝑔\cdot 𝜎𝜐𝜈30^0\cdot 𝑠$$ $$−\dfrac{1}{2}(10\dfrac{m}{s^2})=−(10\dfrac{m}{s^2}\cdot \dfrac{1}{2})\cdot 𝑠−\dfrac{\sqrt{3}}{3}\cdot (10\dfrac{m}{s^2}\cdot \dfrac{\sqrt{3}}{2})\cdot 𝑠 \Rightarrow 𝒔=𝟓\ 𝐦$$
(Μονάδες 3)
4.4
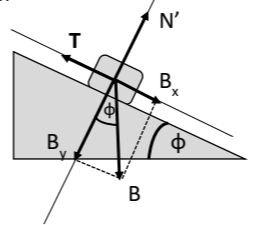
Σχεδιασμός δυνάμεων και ειδικότερα της Τριβής στην ανώτερη θέση, όταν έχει μηδενιστεί η ταχύτητα του σώματος, καθώς το σώμα τείνει να κινηθεί προς τα κάτω.
(Μονάδα 1)
Για να κινηθεί το σώμα προς τα κάτω θα πρέπει \(𝛣_𝑥>𝑇_{𝑜𝜌}=𝛵_{𝜊𝜆}\)
(Μονάδα 1)
$$𝛣_𝑥= 𝑚\cdot 𝑔\cdot 𝜂𝜇30^0=1𝐾𝑔\cdot 10\dfrac{𝑚}{𝑠^2}\cdot \dfrac{1}{2}\Rightarrow𝜝_𝒙=𝟓\ 𝐍$$
$$𝑇_{𝑜𝜌}=𝛵_{𝜊𝜆}= 𝜇\cdot 𝑚\cdot 𝑔\cdot 𝜎𝜐𝜈30^0=\dfrac{\sqrt{3}}{3}\cdot (10\dfrac{𝑚}{𝑠^2}\cdot \dfrac{\sqrt{3}}{2}) \Rightarrow𝑻_{𝒐𝝆}=𝜯_{𝝄𝝀}=𝟓\ 𝐍$$
(Μονάδες 2x2=4)
\(𝜝_𝒙=𝑻_{𝒐𝝆}=𝜯_{𝝄𝝀}\) άρα το σώμα δεν επιστρέφει στην βάση του κεκλιμένου επιπέδου.
(Μονάδα 1)