Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 13944 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 14395 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 28-Φεβ-2024 | Ύλη: | 1.1.8 Η έννοια της επιτάχυνσης στην ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 1.2.4 Ο δεύτερος νόμος του Νεύτωνα ή Θεμελιώδης νόμος της Μηχανικής 1.3.7 Ο νόμος της τριβής 2.1.1 Η έννοια του έργου 2.1.2 Έργο βάρους και μεταβολή της κινητικής ενέργειας | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Φυσική | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 14395 | ||
| Ύλη: | 1.1.8 Η έννοια της επιτάχυνσης στην ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 1.2.4 Ο δεύτερος νόμος του Νεύτωνα ή Θεμελιώδης νόμος της Μηχανικής 1.3.7 Ο νόμος της τριβής 2.1.1 Η έννοια του έργου 2.1.2 Έργο βάρους και μεταβολή της κινητικής ενέργειας | ||
| Τελευταία Ενημέρωση: 28-Φεβ-2024 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Σε σώμα \(Σ\) μάζας \(m=10\ Kg\), το οποίο βρίσκεται στη βάση (θέση \(x_{0}=0\ m\)) μη λείου κεκλιμένου επιπέδου, μεγάλου μήκους και γωνίας κλίσης \(φ=30^{0}\), αρχίζει να ασκείται τη χρονική στιγμή \(t_{0}=0\ s\), σταθερή δύναμη μέτρου \(F=120\ N\), με διεύθυνση παράλληλη του κεκλιμένου επιπέδου, όπως φαίνεται στο σχήμα. To σώμα, ξεκινώντας από την ηρεμία, κινείται κατά μήκος του κεκλιμένου επιπέδου ανεβαίνοντας με σταθερή επιτάχυνση και το μέτρο της μετατόπισής του, κατά τη διάρκεια του 4ου δευτερολέπτου της κίνησής του, είναι \(Δx=7\ m\).
4.1 Nα σχεδιάσετε τις δυνάμεις που ασκούνται στο σώμα κατά την κίνησή του επάνω στο κεκλιμένο επίπεδο, για το χρονικό διάστημα \(t_{0}=0\ s\) έως \(t_{4}=4\ s\) και να τις αναλύσετε σε δύο κάθετους μεταξύ τους άξονες, εκ των οποίων ο ένας να είναι ο άξονας της κίνησης.
Μονάδες 5
Να υπολογίσετε:
4.2 Το μέτρο της επιτάχυνσης του σώματος για το παραπάνω χρονικό διάστημα \(0\ s-4\ s\).
Μονάδες 4
4.3 Τον συντελεστή τριβής ολίσθησης \((μ)\) μεταξύ του σώματος και του κεκλιμένου επιπέδου.
Μονάδες 7
Μετά την χρονική στιγμή \(t_{4}=4\ s\) και ενώ το σώμα βρίσκεται στη θέση \(x_{4}\) επάνω στο κεκλιμένο επίπεδο καταργείται η δύναμη \(\vec{F}\).
4.4 Σε ποια θέση (\(x_{5}\)) θα μηδενιστεί η ταχύτητα του σώματος;
Μονάδες 9
Δίνονται: \(ημ30^{0}=\dfrac{1}{2}\), \(συν30^{0}=\dfrac{\sqrt{3}}{2}\), \(g=10\ \dfrac{m}{s^{2}}\).
Ενδεικτική λύση
4.1
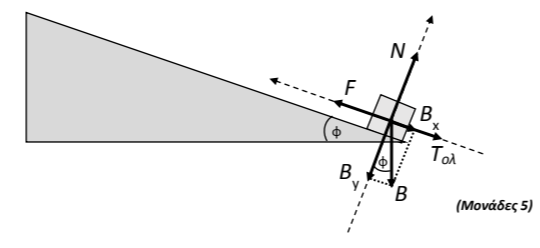
(Mονάδες 5)
4.2
Η μετατόπιση \(Δx\) του σώματος κατά τη διάρκεια του 4ου δευτερολέπτου της κίνησής του προκύπτει από την διαφορά:
$$Δx=x_{4}-x_{3} $$ $$\Rightarrow Δx=\dfrac{1}{2}\cdot a\cdot t_{4}^{2}-\dfrac{1}{2}\cdot a\cdot t_{3}^{2} $$ $$\Rightarrow 7\ m=\dfrac{1}{2}\cdot a\cdot (16-9)\ s^{2} $$ $$\Rightarrow a=2\ \dfrac{m}{s^{2}}$$
(Mονάδες 4)
4.3
Έχουμε:
$$ΣF_{y}=0 $$ $$\Rightarrow N-B_{y}=0 $$ $$\Rightarrow N=m\cdot g\cdot συν30^{0} $$ $$\Rightarrow Ν=10\ Κg\cdot 10\ \dfrac{m}{s^{2}}\cdot \dfrac{\sqrt{3}}{2} $$ $$\Rightarrow N=50\cdot \sqrt{3}\ N\ \ \ \ (1)$$
(Mονάδες 2)
$$Τ_{ολ}=μ\cdot Ν$$
(Mονάδα 1)
$$ΣF_{x}=m\cdot a $$ $$\Rightarrow F-B_{x}-T_{ολ}=m\cdot a $$ $$\Rightarrow F-m\cdot g\cdot ημ30^{0}-μ\cdot Ν=m\cdot a $$ $$\overset{(1)}{\Rightarrow} 120\ Ν-10\ Κg\cdot 10\ \dfrac{m}{s^{2}}\cdot \dfrac{1}{2}-μ\cdot 50\cdot \sqrt{3}=10\ Κg\cdot 2\ \dfrac{m}{s^{2}} $$ $$\Rightarrow μ=\dfrac{\sqrt{3}}{3}$$
(Mονάδες 4)
4.4
To μέτρο της ταχύτητας που θα έχει το σώμα τη χρονική στιγμή \(t_{4}=4\ s\) θα είναι:
$$υ=α\cdot t_{4} $$ $$\Rightarrow υ=2\ \dfrac{m}{s^{2}}\cdot 4\ s $$ $$\Rightarrow υ=8\ \dfrac{m}{s}$$
(Mονάδες 2)
To σώμα θα βρίσκεται στη θέση:
$$x_{4}=\dfrac{1}{2}\cdot a\cdot t_{4}^{2} $$ $$\Rightarrow x_{4}=\dfrac{1}{2}\cdot 2\ \dfrac{m}{s^{2}}\cdot (4\ s)^{2} $$ $$\Rightarrow x_{4}=16\ m$$
(Mονάδες 2)
Εφαρμόζοντας το Θ.Μ.Κ.Ε. από την θέση \(x_{4}\) μέχρι τη θέση \(x_{5}\), που μηδενίζεται η ταχύτητα του σώματος προκύπτει:
$$Κ_{\text{τελ}}-Κ_{\text{αρχ}}=W_{B}+W_{T} $$ $$\Rightarrow 0-\dfrac{1}{2}\cdot m\cdot υ^{2}=-m\cdot g\cdot ημ30^{0}\cdot Δx- μ\cdot Ν\cdot Δx$$ $$\Rightarrow 0-\dfrac{1}{2}\cdot 10\ Kg\cdot (8\ \dfrac{m}{s})^{2}=$$ $$=-10\ Κg\cdot 10\ \dfrac{m}{s^{2}}\cdot \dfrac{1}{2}\cdot Δx-\dfrac{\sqrt{3}}{3}\cdot 50\cdot \sqrt{3}\ N\cdot Δx $$ $$\Rightarrow Δx=3,2\ m$$
(Mονάδες 4)
Άρα η ταχύτητα του σώματος μηδενίζεται στη θέση:
$$x_{5}=x_{4}+Δx $$ $$\Rightarrow x_{5}=16\ m+3,2\ m $$ $$\Rightarrow x_{5}=19,2\ m$$
(Mονάδα 1)