Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 13466 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 14397 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 28-Φεβ-2024 | Ύλη: | 1.1.5. Η έννοια της ταχύτητας στη ευθύγραμμη ομαλή κίνηση 1.1.8 Η έννοια της επιτάχυνσης στην ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 1.2.4 Ο δεύτερος νόμος του Νεύτωνα ή Θεμελιώδης νόμος της Μηχανικής 1.3.6 Ισορροπία ομοεπιπέδων δυνάμεων 1.3.7 Ο νόμος της τριβής 2.1.1 Η έννοια του έργου 2.1.2 Έργο βάρους και μεταβολή της κινητικής ενέργειας | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Φυσική | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 14397 | ||
| Ύλη: | 1.1.5. Η έννοια της ταχύτητας στη ευθύγραμμη ομαλή κίνηση 1.1.8 Η έννοια της επιτάχυνσης στην ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 1.2.4 Ο δεύτερος νόμος του Νεύτωνα ή Θεμελιώδης νόμος της Μηχανικής 1.3.6 Ισορροπία ομοεπιπέδων δυνάμεων 1.3.7 Ο νόμος της τριβής 2.1.1 Η έννοια του έργου 2.1.2 Έργο βάρους και μεταβολή της κινητικής ενέργειας | ||
| Τελευταία Ενημέρωση: 28-Φεβ-2024 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Σώμα μάζας \(m=20\ Kg\) είναι ακίνητο επάνω σε ένα οριζόντιο δάπεδο, στη θέση \(x_{0}=0\ m\). Τη χρονική στιγμή \(t_{0}=0\ s\), στο σώμα ασκείται οριζόντια δύναμη μέτρου \(F=80\ N\) και αυτό αρχίζει να κινείται με σταθερή επιτάχυνση. Το σώμα την χρονική στιγμή \(t_{1}=6\ s\) φθάνει στη θέση \(x_{1}=45\ m\).
Η επιτάχυνση της βαρύτητας δίνεται \(g=10\ \dfrac{m}{s^{2}}\).
4.1 Να υπολογίσετε την επιτάχυνση του σώματος και την ταχύτητά του την χρονική στιγμή \(t_{1}=6\ s\).
Μονάδες 6
4.2 Να δικαιολογήσετε, ότι μεταξύ του δαπέδου και του σώματος ασκείται δύναμη τριβής ολίσθησης, να σχεδιάσετε όλες τις δυνάμεις που ασκούνται στο σώμα και να υπολογίσετε την τιμή του αντίστοιχου συντελεστή \((μ)\).
Μονάδες 10
Μετά την χρονική στιγμή \(t_{1}=6\ s\) το σώμα συνεχίζει την κίνησή του επάνω στο οριζόντιο δάπεδο, ενώ εξακολουθεί να ασκείται σ’ αυτό η δύναμη \(\vec{F}\) και την χρονική στιγμή \(t_{2}=10\ s\) φθάνει στη θέση \(x_{2}=137\ m\).
4.3 Υπάρχει δύναμη τριβής ολίσθησης από τη θέση \(x_{1}\) μέχρι τη θέση \(x_{2}\);
Να δικαιολογήσετε την απάντησή σας.
Μονάδες 4
4.4 Να υπολογίσετε τα έργα όλων των δυνάμεων που ασκούνται στο σώμα από την θέση \(x_{0}=0\ m\) μέχρι την θέση \(x_{2}=137\ m\) και να σχεδιάσετε το διάγραμμα επιτάχυνσης – χρόνου από την χρονική στιγμή \(t_{0}=0\ s\) μέχρι την χρονική στιγμή \(t_{2}=10\ s\).
Μονάδες 7
Ενδεικτική λύση
4.1
Από τις εξισώσεις θέσης και ταχύτητας στην ευθύγραμμη ομαλά επιταχυνόμενη κίνηση έχουμε:
$$x_{1}=\dfrac{1}{2}\cdot a\cdot t_{1}^{2} $$ $$\Rightarrow 45\ m=\dfrac{1}{2}\cdot a\cdot (6\ s)^{2} $$ $$\Rightarrow a=2,5\ \dfrac{m}{s^{2}}$$
(Μονάδες 3)
$$υ_{1}=α\cdot t_{1}=2,5\ \dfrac{m}{s^{2}}\cdot 6\ s $$ $$\Rightarrow υ_{1}=15\ \dfrac{m}{s}$$
(Μονάδες 3)
4.2
Αν δεν ασκείται δύναμη τριβής ολίσθησης μεταξύ του σώματος και του δαπέδου τότε:
$$ΣF=F=m\cdot α' $$ $$\Rightarrow α'=\dfrac{F}{m} $$ $$\Rightarrow α'=\dfrac{80\ N}{20\ Kg} $$ $$\Rightarrow α'=4\ \dfrac{m}{s^{2}}$$
H επιτάχυνση του σώματος, που υπολογίσαμε στο προηγούμενο ερώτημα 4.1, σύμφωνα με τα δεδομένα του προβλήματος είναι:
$$α=2,5\ \dfrac{m}{s^{2}} < α ' $$
(Μονάδες 3)
Άρα το σώμα δέχεται δύναμη τριβή ολίσθησης, επομένως:
$$ΣF=F-Τ_{ολ}=m\cdot α $$ $$\Rightarrow 80\ Ν-Τ_{ολ}=20\ Kg\cdot 2,5\ \dfrac{m}{s^{2}} $$ $$\Rightarrow Τ_{ολ}=30\ Ν$$
(Μονάδες 2)
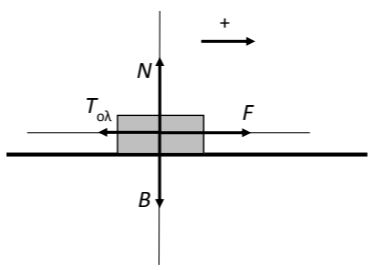
(Μονάδες 3)
$$Τ_{ολ}=μ\cdot Ν=μ\cdot m\cdot g $$ $$\Rightarrow μ=\dfrac{30\ Ν}{20\ Κg\cdot 10\ \dfrac{m}{s^{2}}} $$ $$\Rightarrow μ=0,15$$
(Μονάδες 2)
4.3
Από τη θέση \(x_{1}=45\ m\) μέχρι τη θέση \(x_{2}=137\ m\) η τιμή της μετατόπισης του σώματος είναι
$$Δx=92\ m$$
και η χρονική διάρκεια της κίνησης
$$Δt=t_{2}-t_{1}=10\ s-6\ s $$ $$\Rightarrow Δt=4\ s$$
επομένως:
$$Δx=υ_{1}\cdot Δt+\dfrac{1}{2}\cdot a_{1}\cdot (Δt)^{2} $$ $$\Rightarrow 92\ m=15\ \dfrac{m}{s}\cdot 4\ s+\dfrac{1}{2}\cdot a_{1}\cdot (4\ s)^{2} $$ $$\Rightarrow a_{1}=4\ \dfrac{m}{s^{2}}$$
Με το δεδομένο ότι δεν έχει καταργηθεί η δύναμη \(\vec{F}\) και συγκρίνοντας την τιμή της επιτάχυνσης \(a_{1}\) με την \(a'\) (απάντηση ερωτήματος 4.2) συμπεραίνουμε ότι αυτό το τμήμα του δαπέδου είναι λείο.
(Μονάδες 4)
4.4
Τα ζητούμενα έργα είναι:
$$W_{F}=F\cdot (x_{2}-x_{0}) $$ $$\Rightarrow W_{F}=80\ N\cdot 137\ m $$ $$\Rightarrow W_{F}=10960\ J$$
$$W_{ολ}=-Τ_{ολ}\cdot (x_{1}-x_{0}) $$ $$\Rightarrow W_{ολ}=-30\ N\cdot 45\ m $$ $$\Rightarrow W_{ολ}=-1350\ J$$
$$W_{Β}=W_{Ν}=0\ J$$
(Μονάδες 4)

(Μονάδες 3)
