Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 18459 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Άλγεβρα | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 14813 | Θέμα: | 1 | |
| Τελευταία Ενημέρωση: | 29-Αυγ-2023 | Ύλη: | 2.4. Ρίζες Πραγματικών Αριθμών 3.1. Εξισώσεις 1ου Βαθμού 4.2. Ανισώσεις 2ου Βαθμού 5.2. Αριθμητική πρόοδος 6.1. Η Έννοια της Συνάρτησης 6.2. Γραφική Παράσταση Συνάρτησης | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Άλγεβρα | ||
| Θέμα: | 1 | ||
| Κωδικός Θέματος: | 14813 | ||
| Ύλη: | 2.4. Ρίζες Πραγματικών Αριθμών 3.1. Εξισώσεις 1ου Βαθμού 4.2. Ανισώσεις 2ου Βαθμού 5.2. Αριθμητική πρόοδος 6.1. Η Έννοια της Συνάρτησης 6.2. Γραφική Παράσταση Συνάρτησης | ||
| Τελευταία Ενημέρωση: 29-Αυγ-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 1
Α1. Στις τέσσερις πρώτες ερωτήσεις να γράψετε στην κόλλα σας το γράμμα Σ αν η πρόταση είναι σωστή ή το γράμμα Λ αν η πρόταση είναι λάθος, μετά από τον αριθμό της ερώτησης. Στην πέμπτη ερώτηση να γράψετε το γράμμα της σωστής απάντησης μετά από τον αριθμό της ερώτησης.
- Αν \(α\le 0\) και \(ν\) άρτιος, τότε ισχύει \(\sqrt[ν]{α^{ν}}=|α|\).
- Η γραφική παράσταση μιας συνάρτησης \(f(x)\) μπορεί να τέμνει τον άξονα \(y'y\) σε ακριβώς δύο σημεία.
- Θεωρούμε την αριθμητική πρόοδο \((α_{ν})\) με πρώτο όρο \(α_{1}\) και διαφορά \(ω\). Το άθροισμα \(S_{ν}\) των \(ν\) πρώτων διαδοχικών όρων της \((α_{ν})\) δίνεται από την σχέση \(S_{ν}=\dfrac{ν}{2}[α_{1}+(ν-1)ω]\).
- Η εξίσωση \(α\cdot x+β=0\) είναι αδύνατη ως προς \(x\), όταν \(α = 0\) και \(β \ne 0\).
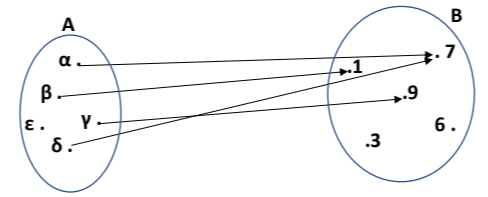
Στο παραπάνω σχήμα δίνεται μια αντιστοιχία στοιχείων ενός συνόλου \(Α\) σε στοιχεία ενός συνόλου \(Β\). Ποιο από τα παρακάτω είναι σωστό;
Α) η αντιστοιχία αυτή παριστάνει συνάρτηση από το σύνολο \(Α\) στο σύνολο \(Β\).
Β) η αντιστοιχία αυτή δεν παριστάνει συνάρτηση διότι στο \(3\) και στο \(6\) δεν αντιστοιχεί κανένα στοιχείο του \(Α\).
Γ) η αντιστοιχία αυτή δεν παριστάνει συνάρτηση διότι τα διαφορετικά στοιχεία \(α\) και \(δ\) του συνόλου \(Α\) αντιστοιχούν στο ίδιο στοιχείο του συνόλου \(Β\), το \(7\).
Δ) η αντιστοιχία αυτή δεν παριστάνει συνάρτηση διότι το στοιχείο \(ε\) δεν αντιστοιχεί σε κανένα στοιχείο του \(Β\).
(Μ10)
Α2. Έστω \(x_{1},x_{2}\) με \(x_{1}<x_{2}\) είναι οι δύο πραγματικές ρίζες του τριωνύμου \(f(x)=αx^{2}+ βx+γ\), \(x\in \mathbb{R}\). Να αποδείξετε ότι, αν για την μεταβλητή \(x\) ισχύει \(x<x_{1}\) ή \(x>x_{2}\) τότε τότε το τριώνυμο \(f(x)\) γίνεται ομόσημο του \(α\).
(Μ15)
ΑΠΑΝΤΗΣΕΙΣ
A1.
- Σ ii) Λ iii) Λ iv) Σ v) Δ
Α2. Απόδειξη σελ. 108 σχολ. βιβλ.