Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 6894 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Γεωμετρία | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 14886 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 04-Απρ-2023 | Ύλη: | 4.6. Άθροισμα γωνιών τριγώνου 5.3. Ορθογώνιο 5.6. Εφαρμογές στα τρίγωνα 5.9. Μια ιδιότητα του ορθογώνιου τριγώνου | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Γεωμετρία | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 14886 | ||
| Ύλη: | 4.6. Άθροισμα γωνιών τριγώνου 5.3. Ορθογώνιο 5.6. Εφαρμογές στα τρίγωνα 5.9. Μια ιδιότητα του ορθογώνιου τριγώνου | ||
| Τελευταία Ενημέρωση: 04-Απρ-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Θεωρούμε ένα ορθογώνιο τρίγωνο \(ΑΒΓ\) (\(\hat{Α}=90^0\)), τα μέσα \(Δ\), \(Ε\), \(Ζ\) των πλευρών του και το ύψος του \(ΑΚ\). Αν \(Θ\) είναι το σημείο τομής των \(ΑΖ\) και \(ΔΕ\), τότε:
α) Να αποδείξετε ότι:
- Το τετράπλευρο \(ΑΔΖΕ\) είναι ορθογώνιο.
(Μονάδες 8) - \(ΑΘ=ΘΕ=\dfrac{ΒΓ}{4}\)
(Μονάδες 7)
β) Αν επιπλέον είναι \(\hat{Γ}= 30^0\), τότε:
- να βρείτε τη γωνία \(\hat{ΑΖΒ}\).
(Μονάδες 5) - να αποδείξετε ότι \(ΒΚ =\dfrac{ΒΓ}{4}\).
(Μονάδες 5)
α)
i.
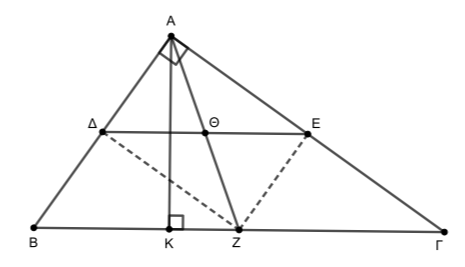
Tο τμήμα \(ΕΖ\) ενώνει τα μέσα των πλευρών \(ΑΓ\) και \(ΒΓ\) στο τρίγωνο \(ΑΒΓ\), άρα \(ΕΖ \parallel ΑΒ\) οπότε και \(ΕΖ \parallel ΑΔ\) και \(ΕΖ =\dfrac{AB}{2} = ΑΔ\). Άρα το τετράπλευρο \(ΑΔΖΕ\) έχει τις απέναντι πλευρές του \(ΑΔ\) και \(ΕΖ\) ίσες και παράλληλες οπότε είναι παραλληλόγραμμο. Επιπλέον η γωνία του \(\hat{Α}\) είναι ορθή, άρα το τετράπλευρο \(ΑΔΖΕ\) είναι ορθογώνιο.
ii.Το τμήμα \(ΔΕ\) ενώνει τα μέσα των πλευρών \(ΑΒ\) και \(ΑΓ\) στο τρίγωνο \(ΑΒΓ\), οπότε \(ΔΕ \parallel ΒΓ\) και \(ΔΕ =\dfrac{ΒΓ}{2}\).
Οι \(ΑΖ\), \(ΔΕ\) είναι διαγώνιες του ορθογωνίου \(ΑΔΖΕ\), οπότε είναι ίσες και διχοτομούνται με \(Θ\) το κέντρο του. Άρα \(ΑΘ =\dfrac{ΑΖ}{2} = \dfrac{ΔΕ}{2}= ΘΕ\). Το ευθύγραμμο τμήμα \(ΘΕ\) ενώνει τα μέσα των \(ΑΖ\) και \(ΑΓ\) στο τρίγωνο \(ΑΖΓ\), άρα \(ΘΕ = \dfrac{ΖΓ}{2} = \dfrac{\dfrac{ΒΓ}{2}}{2} = \dfrac{ΒΓ}{4}\).
β)
i.Επειδή \(\hat{ΖΕΓ}= 90^0\), το \(ΖΕ\) είναι ύψος στο τρίγωνο \(ΑΖΓ\) και επειδή είναι και διάμεσος, το τρίγωνο είναι ισοσκελές. Άρα \(\hat{ΖΑΓ}= \hat{Γ} = 30^0\).
Η γωνία \(\hat{ΑΖΒ}\) είναι εξωτερική στο τρίγωνο \(ΑΖΓ\), άρα: \(\hat{ΑΖΒ} = \hat{ΖΑΓ} + \hat{Γ} = 60^0\).
ii.Στο ορθογώνιο τρίγωνο \(ΑΒΓ\) είναι \(\hat{Γ}= 30^0\), άρα \(AB =\dfrac{ΒΓ}{2}\) (1). Από το άθροισμα γωνιών του ορθογωνίου τριγώνου \(ΑΒΓ\), έχουμε: \(\hat{Β} + \hat{Γ} = 90^0\) ή \(\hat{Β}= 60^0\). Από το άθροισμα γωνιών του ορθογωνίου τριγώνου \(ΑΚΒ\) έχουμε: \(\hat{BΑK} + \hat{Β} = 90^0\) ή \(\hat{BΑK} = 30^0\). Οπότε στο ορθογώνιο τρίγωνο \(ΑΒΚ\) είναι \(BΚ =\dfrac{ΑΒ}{2}\) και λόγω της (1) \(ΒΚ = \dfrac{\dfrac{ΒΓ}{2}}{2}\) ή \(ΒΚ=\dfrac{ΒΓ}{4}\).
