Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 49261 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Άλγεβρα | Τάξη: | Β' Λυκείου | |
| Κωδικός Θέματος: | 15679 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 08-Οκτ-2024 | Ύλη: | 4.4 Εξισώσεις και ανισώσεις που ανάγονται σε πολυωνυμικές 5.1 Εκθετική συνάρτηση 5.2 Λογάριθμοι 5.3 Λογαριθμική συνάρτηση | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Β' Λυκείου | ||
| Μάθημα: | Άλγεβρα | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 15679 | ||
| Ύλη: | 4.4 Εξισώσεις και ανισώσεις που ανάγονται σε πολυωνυμικές 5.1 Εκθετική συνάρτηση 5.2 Λογάριθμοι 5.3 Λογαριθμική συνάρτηση | ||
| Τελευταία Ενημέρωση: 08-Οκτ-2024 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Δίνεται η παράσταση \(Α=\ln(\frac{e^{2x}-1}{e^{x}-3})\)
α) Να λύσετε την ανίσωση \(\frac{ω^2-1}{ω-3}>0\)
(Μονάδες 8)
β) Να βρείτε για ποιες τιμές του x ορίζεται η παράσταση Α.
(Μονάδες 8)
γ) Να λύσετε την εξίσωση \(Α=-\ln3.\)
(Μονάδες 9)
ΛΥΣΗ
α) Η ανίσωση \(\frac{ω^2-1}{ω-3}>0\) με \(ω\neq3\) είναι ισοδύναμη με την \((ω^2-1)(ω-3)>0\).
Το πρόσημο του \((ω^2-1)(ω-3)\) φαίνεται στον παρακάτω πίνακα.
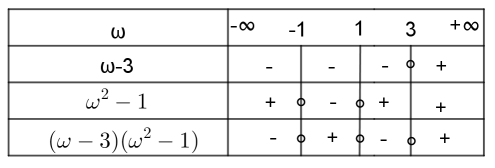
Συνεπώς, η ανίσωση \(\frac{ω^2-1}{ω-3}>0\) αληθεύει για κάθε \(ω\in(-1,1)\cup(3,+\infty)\).
β) Η παράσταση \(Α\) ορίζεται για κάθε πραγματική τιμή του \(x\) για την οποία ισχύει \(\frac{e^{2x}-1}{e^{x}-3}>0\).
Αν θέσουμε \(e^x=ω\) η ανίσωση \(\frac{e^{2x}-1}{e^{x}-3}>0\) γίνεται \(\frac{ω^2-1}{ω-3}>0\) που όπως δείξαμε στο α) αληθεύει για \(ω\in(-1,1)\cup(3,+\infty)\).
Συνεπώς θα πρέπει \(-1<ω<1\Leftrightarrow -1<e^x<1 \Leftrightarrow x<0\)
ή \(ω>3\Leftrightarrow e^x>3 \Leftrightarrow x>\ln3\)
Τελικά η παράσταση \(Α\) ορίζεται για κάθε \(x\in(-\infty,0)\cup(\ln3,+\infty)\).
γ) Η εξίσωση \(Α=-\ln3\) ορίζεται για κάθε \(x\in(-\infty,0)\cup(\ln3,+\infty)\) και γίνεται ισοδύναμα:
\begin{align} & \ln \Big(\frac{e^{2x}-1}{e^{x}-3} \Big)=\ln3^{-1} \\ \Leftrightarrow & \frac{e^{2x}-1}{e^{x}-3}=\frac{1}{3} \\ \Leftrightarrow & 3e^{2x}-3=e^x-3 \\ \Leftrightarrow & 3e^{2x}-e^x=0 \\ \Leftrightarrow & e^x(3e^x-1)=0 \\ \Leftrightarrow & 3e^x-1=0 \\ \Leftrightarrow & e^x=\frac{1}{3} \\ \Leftrightarrow & x=\ln\frac{1}{3} \end{align}
και επειδή \(\frac{1}{3}<1 \Leftrightarrow \ln\frac{1}{3}<0\) η λύση \(x=\ln\frac{1}{3}\) είναι δεκτή.