Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 49745 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική Προσανατολισμού | Τάξη: | Β' Λυκείου | |
| Κωδικός Θέματος: | 16044 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 26-Αυγ-2022 | Ύλη: | 1.1 Οριζόντια βολή 2.5 Η αρχή διατήρησης της ορμής | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Β' Λυκείου | ||
| Μάθημα: | Φυσική Προσανατολισμού | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 16044 | ||
| Ύλη: | 1.1 Οριζόντια βολή 2.5 Η αρχή διατήρησης της ορμής | ||
| Τελευταία Ενημέρωση: 26-Αυγ-2022 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
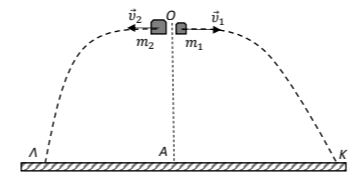
Μία οβίδα μάζας \(3\ 𝑘𝑔\) εκτοξεύεται από το σημείο Α του οριζόντιου εδάφους κατακόρυφα προς τα πάνω.
Όταν φθάνει στο ανώτερο σημείο O της τροχιάς της, διασπάται ακαριαία, λόγω εσωτερικής έκρηξης, σε δύο κομμάτια με μάζες \(𝑚_{1}=1\ 𝑘𝑔\) και \(𝑚_{2}=2\ 𝑘𝑔\).
Το σημείο \(Ο\) βρίσκεται σε ύψος \(20\ 𝑚\) από το έδαφος.
Το κομμάτι μάζας \(𝑚_{1}\) αποκτά αμέσως μετά την έκρηξη οριζόντια ταχύτητα μέτρου \(𝜐_{1}=10\ 𝑚/𝑠\) όπως φαίνεται στο σχήμα.
Τα κομμάτια \(𝑚_{1}\) και \(𝑚_{2}\) κινούνται και πέφτουν στο έδαφος σε σημεία \(Κ\) και \(Λ\) αντιστοίχως.
Να υπολογίσετε:
4.1. Το μέτρο και την κατεύθυνση της ταχύτητας που αποκτά το κομμάτι μάζας \(𝑚_{2}\) αμέσως μετά την έκρηξη.
Μονάδες 7
4.2. Το χρονικό διάστημα που κινείται κάθε κομμάτι από τη στιγμή της έκρηξης μέχρι να αγγίξει το έδαφος.
Μονάδες 6
4.3. Την απόσταση \(ΚΛ\).
Μονάδες 7
4.4 Την ταχύτητα (μέτρο και κατεύθυνση) του κομματιού μάζας \(m_{1}\) ακριβώς πριν ακουμπήσει στο σημείο \(Κ\) του εδάφους.
Δίνεται η επιτάχυνση της βαρύτητας στην επιφάνεια της Γης \(𝑔=10\ 𝑚/𝑠^{2}\), και ότι η αντίσταση του αέρα θεωρείται αμελητέα.
ΘΕΜΑ 4
4.1. Η οβίδα στο ανώτερο σημείο της τροχιάς της (\(O\)) ακινητοποιείται στιγμιαία οπότε ακριβώς πριν την διάσπαση έχει μηδενική ταχύτητα και ορμή.
Κατά την έκρηξη που διαρκεί ελάχιστο χρόνο οι εσωτερικές δυνάμεις που αναπτύσσονται είναι πολύ μεγαλύτερες του βάρους (εξωτερική δύναμη), οπότε το σύστημα θεωρείται μονωμένο και η ορμή του διατηρείται:
$$\vec{p}_{πριν}=\vec{p}_{μετά}$$
Λαμβάνοντας ως θετική τη φορά της ταχύτητας του κομματιού με μάζα \(𝑚_{1}\) αμέσως μετά την έκρηξη:
$$0=𝑚_{1}\cdot 𝜐_{1}−𝑚_{2}\cdot 𝜐_{2}$$ $$\Rightarrow 𝜐_{2}=\dfrac{𝑚_{1}\cdot 𝜐_{1}}{𝑚_{2}}$$ $$\Rightarrow 𝜐_{2}=5\ 𝑚/𝑠$$
Άρα η ταχύτητα που αποκτά το κομμάτι μάζας \(𝑚_{2}\) αμέσως μετά την έκρηξη έχει μέτρο \(5\ 𝑚/𝑠\) και κατεύθυνση αντίθετη της \(\vec{u_{1}}\).
Μονάδες 7
4.2. Το κάθε κομμάτι εκτελεί οριζόντια βολή. Σύμφωνα με την αρχή ανεξαρτησίας των κινήσεων η κίνηση τους προκύπτει από την επαλληλία μίας ελεύθερης πτώσης στον κατακόρυφο άξονα και μίας ευθύγραμμης ομαλής στον οριζόντιο.
Το χρονικό διάστημα που πέρασε από την στιγμή της κρούσης μέχρι το κάθε κομμάτι να αγγίξει το έδαφος \(𝛥𝑡_{𝜋}\) είναι το ίδιο και για τα δύο καθώς βάλλονται ταυτόχρονα από το ίδιο ύψος.
Το \(𝛥𝑡_{𝜋}\) υπολογίζεται από την εξίσωση κίνησης της ελεύθερης πτώσης για ύψος \((𝛰𝛢)=ℎ = 20\ 𝑚\):
$$ℎ=\dfrac{1}{2}\cdot 𝑔\cdot 𝛥𝑡_{𝜋}^{2}$$ $$\Rightarrow 𝛥𝑡_{𝜋} =\sqrt{\dfrac{2\cdot ℎ}{𝑔}}$$ $$\Rightarrow 𝛥𝑡_{𝜋}=2\ 𝑠$$
Μονάδες 6
4.3. Κατά την οριζόντια βολή η τροχιά είναι παραβολική. Η εξίσωση κίνησης της ευθύγραμμης ομαλής υπολογίζει την μέγιστη οριζόντια απόσταση (βεληνεκές) για κάθε κομμάτι μετά τη διάσπαση. Συγκεκριμένα:
Κομμάτι μάζας \(𝑚_{1}\):
$$(𝛢𝛫)=𝜐_{1}\cdot 𝛥𝑡_{𝜋} =20\ 𝑚$$
Κομμάτι μάζας \(𝑚_{2}\):
$$(𝛢𝛬)=𝜐_{2}\cdot 𝛥𝑡_{𝜋} =10\ 𝑚$$
Άρα:
$$(𝛫𝛬)=(𝛢𝛫)+(𝛢𝛬)=30\ 𝑚$$
Μονάδες 7
4.4
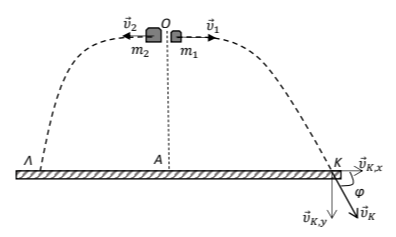
Σύμφωνα με την αρχή ανεξαρτησίας των κινήσεων η ταχύτητα πρόσκρουσης του κομματιού με μάζα \(𝑚_{1}\) στο σημείο \(Κ\) προκύπτει από το διανυσματικό άθροισμα των ταχυτήτων στον κατακόρυφο άξονα (ελεύθερη πτώση) και στον οριζόντιο άξονα (ευθύγραμμη ομαλή κίνηση).
Οριζόντιος άξονας:
$$𝜐_{𝛫,𝑥}=𝜐_{1}=10\ 𝑚/𝑠$$
Κατακόρυφος άξονας:
$$𝜐_{𝛫,𝑦}=𝑔\cdot 𝛥𝑡_{𝜋} =20\ 𝑚/𝑠$$
Οπότε,
$$𝜐_{𝛫}=\sqrt{𝜐_{𝛫,𝑥}^{2}+𝜐_{𝛫,𝑦}^{2}}$$ $$\Rightarrow 𝜐_{𝛫}=\sqrt{500}\ 𝑚/𝑠$$ $$\Rightarrow 𝜐_{𝛫}=10\cdot \sqrt{5}\ 𝑚/𝑠\ \text{(μέτρο)}$$
Και
$$𝜀𝜑φ=\dfrac{𝜐_{𝛫,𝑦}}{𝜐_{𝛫,𝑥}}=2\ \text{(κατεύθυνση)}$$
Μονάδες 5
