Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 30809 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική Προσανατολισμού | Τάξη: | Β' Λυκείου | |
| Κωδικός Θέματος: | 16045 | Θέμα: | 2 | |
| Τελευταία Ενημέρωση: | 25-Αυγ-2022 | Ύλη: | 2.4 Η δύναμη και η μεταβολή της ορμής 3.2 Νόμοι αερίων | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Β' Λυκείου | ||
| Μάθημα: | Φυσική Προσανατολισμού | ||
| Θέμα: | 2 | ||
| Κωδικός Θέματος: | 16045 | ||
| Ύλη: | 2.4 Η δύναμη και η μεταβολή της ορμής 3.2 Νόμοι αερίων | ||
| Τελευταία Ενημέρωση: 25-Αυγ-2022 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 2
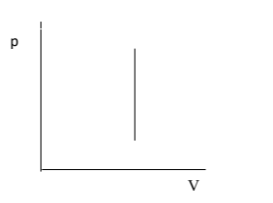
2.1. Δίνεται το διάγραμμα \((p - V)\) το οποίο απεικονίζει μια μεταβολή ιδανικού αερίου.
Παρακάτω δίνονται τρεις πειραματικές διατάξεις που χρησιμοποιούνται για πειράματα με μονοατομικά αέρια που με καλή προσέγγιση θεωρούνται ιδανικά.
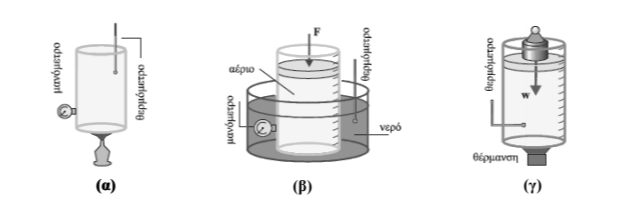
Ποια από αυτές θα προκαλέσει μεταβολή στο μονοατομικό αέριο που περιέχει, αντίστοιχη με αυτή που παριστάνεται γραφικά στο διάγραμμα;
2.1.Α. Να επιλέξετε την κατάλληλη διάταξη.
Μονάδες 4
2.1.B. Να αιτιολογήσετε την επιλογή σας.
Μονάδες 8
2.2. Ένα βλήμα μάζας \(0,05\ kg\) κινείται οριζόντια με ταχύτητα \(800\ \dfrac{m}{s}\) μέχρι τη στιγμή που σφηνώνεται σε τοίχο.
Πριν ακινητοποιηθεί το βλήμα διανύει απόσταση \(8\ cm\) μέσα στον τοίχο.
Αν η αντίσταση του τοίχου θεωρηθεί σταθερή δύναμη, το βλήμα θα ακινητοποιηθεί μετά από χρονικό διάστημα:
(α) \(Δ𝑡=2\cdot 10^{−2}\ 𝑠\)
(β) \(Δ𝑡=2\cdot 10^{−3}\ 𝑠\)
(γ) \(Δ𝑡=2\cdot 10^{−4}\ 𝑠\)
2.2.Α. Να επιλέξετε τη σωστή απάντηση.
Μονάδες 4
2.2.B. Να αιτιολογήσετε την επιλογή σας.
Μονάδες 9
ΘΕΜΑ 2
2.1.
2.1.Α. Σωστή απάντηση η (α)
Μονάδες 4
2.1.B. Παρατηρούμε ότι κατά τη διάρκεια της μεταβολής στο διάγραμμα ο όγκος παραμένει σταθερός όσο μεταβάλλεται η πίεση.
Άρα πρόκειται για μια ισόχωρη μεταβολή.
Μονάδες 8
2.2.
2.2.A. Σωστή απάντηση η (γ)
Μονάδες 4
2.2.B.
Α΄ τρόπος (χωρίς χρήση της μάζας)
Αφού η δύναμη από τον τοίχο θεωρείται σταθερή, το βλήμα επιβραδύνεται ομαλά μέχρι να ακινητοποιηθεί. Άρα η χρονική διάρκεια \(Δt_{\text{stop}}\) της ακινητοποίησής του υπολογίζεται από τον τύπο της κινηματικής:
$$Δt_{\text{stop}}=\dfrac{υ_{ο}}{|α|}$$
Το μέτρο της επιβράδυνσης υπολογίζεται από την σχέση:$$Δx_{\text{stop}}=\dfrac{υ_{o}^{2}}{2|α|}$$ $$|α|=\dfrac{υ_{o}^{2}}{2\cdot x_{\text{stop}}}$$
Συνδυάζοντας τις δύο σχέσεις έχουμε:
$$\begin{align} Δt_{\text{stop}}&=\dfrac{υ_{ο}}{\dfrac{υ_{o}^{2}}{2\cdot Δx_{\text{stop}}}}\Leftrightarrow\\ Δt_{\text{stop}}&=\dfrac{2\cdot Δx_{\text{stop}}\cdot υ_{ο}}{υ_{o}^{2}}\Leftrightarrow\\ Δt_{\text{stop}}&=\dfrac{2\cdot Δx_{\text{stop}}}{υ_{ο}}\Leftrightarrow\\ Δt_{\text{stop}}&=\dfrac{2\cdot 8\cdot 10^{-2}}{800}\ s\Leftrightarrow\\ Δt_{\text{stop}}&=\dfrac{2\cdot 8\cdot 10^{-2}}{8\cdot 10^{2}}\ s\Leftrightarrow\\ Δt_{\text{stop}}&=\dfrac{2\cdot 10^{-2}}{10^{2}}\ s \end{align}$$
$$Δt_{\text{stop}}=2\cdot 10^{-4}s$$
Μονάδες 9
Β΄ τρόπος (με χρήση της μάζας)
Από τον 2ο νόμο του Newton έχουμε:
$$\vec{F}=\dfrac{\vec{P}_{\text{τελ}}-\vec{P}_{\text{αρχ}}}{Δt_{\text{stop}}}\ \ \text{(1)}$$
Το μέτρο της δύναμης μπορούμε να το υπολογίσουμε από το θεώρημα έργου-ενέργειας:
$$\begin{align}ΔΚ&=W_{F}\Leftrightarrow\\ Κ_{\text{τελ}}-Κ_{\text{αρχ}}&=-F\cdot Δx_{\text{stop}}\Leftrightarrow\\ -\dfrac{1}{2}mυ^{2}&= -F\cdot Δx_{\text{stop}}\Leftrightarrow\\ F&=\dfrac{mυ^{2}}{2\cdot Δx_{\text{stop}}}\Leftrightarrow\\ F&=\dfrac{0,05\cdot 800^{2}}{2\cdot 8\cdot 10^{-2}}\ Ν\Leftrightarrow\\ F&=\dfrac{5\cdot 10^{-2}\cdot 800^{2}}{2\cdot 8\cdot 10^{-2}}\ Ν\Leftrightarrow\\ F&=\dfrac{5\cdot 800\cdot 800}{2\cdot 8}\ Ν\Leftrightarrow\\ F&=5\cdot 400\cdot 100\ Ν \end{align}$$
Τελικά:$$F=200.000\ Ν$$
Άρα από (1) προκύπτει ότι:
$$\begin{align} Δt&=\dfrac{m\cdot υ}{F}\\ &=\dfrac{5\cdot 10^{-2}\cdot 800}{200.000}\ s\\ &=\dfrac{5\cdot 8}{200.000}\ s\\ &=\dfrac{40}{200.000}\ s\\ &=\dfrac{4}{20.000}\ s\\ &=\dfrac{2}{10.000}\ s\\ &=0,0002\ s \end{align}$$
ή
$$Δt=2\cdot 10^{-4}\ s$$
Μονάδες 9