Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 41057 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική Προσανατολισμού | Τάξη: | Β' Λυκείου | |
| Κωδικός Θέματος: | 16074 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 29-Οκτ-2022 | Ύλη: | 1.2 Ομαλή κυκλική κίνηση 1.3 Κεντρομόλος δύναμη 5.12 Το βαρυτικό πεδίο 5.13 Το βαρυτικό πεδίο της Γης 5.14 Ταχύτητα διαφυγής-Μαύρες τρύπες | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Β' Λυκείου | ||
| Μάθημα: | Φυσική Προσανατολισμού | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 16074 | ||
| Ύλη: | 1.2 Ομαλή κυκλική κίνηση 1.3 Κεντρομόλος δύναμη 5.12 Το βαρυτικό πεδίο 5.13 Το βαρυτικό πεδίο της Γης 5.14 Ταχύτητα διαφυγής-Μαύρες τρύπες | ||
| Τελευταία Ενημέρωση: 29-Οκτ-2022 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Ένα σώμα μάζας \(m_{1}\) περιστρέφεται σε κυκλική τροχιά σε ύψος \(h=\dfrac{7}{9}R_{Γ}\) από την επιφάνεια της Γης υπό την επίδραση μόνο της βαρυτικής έλξης της Γης. Ένα άλλο σώμα μάζας \(m_{2}=2m_{1}\) που περιστρέφεται κατά την αντίθετη φορά στην ίδια κυκλική τροχιά υπό την επίδραση μόνο της βαρυτικής έλξης της Γης, συγκρούεται πλαστικά με το σώμα μάζας \(m_{1}\). Η αντίσταση του αέρα θεωρείται αμελητέα.
Δίνονται: η ακτίνα της Γης \(R_{Γ}=6400\ Km\) και το μέτρο της επιτάχυνσης της βαρύτητας στην επιφάνεια της Γης \(g_{0}=10\ \dfrac{m}{s^{2}}\).
4.1. Να υπολογίσετε την ταχύτητα περιστροφής κάθε σώματος πριν συγκρουστούν.
Μονάδες 6
4.2. Να υπολογίσετε την περίοδο περιστροφής κάθε σώματος πριν συγκρουστούν.
Δίνεται ότι: \(\dfrac{1024π}{27}=119,15\)
Μονάδες 6
4.3. Να υπολογίσετε την ταχύτητα του συσσωματώματος αμέσως μετά τη δημιουργία του.
Μονάδες 6
4.4. Να ελέγξετε αν το συσσωμάτωμα διαφεύγει από το βαρυτικό πεδίο της Γης.
Μονάδες 7
ΘΕΜΑ 4
4.1. H βαρυτική έλξη \(\vec{F}_{g}\) που δέχεται το σώμα μάζας \(m_{1}\) από τη Γη δρα σαν κεντρομόλος:
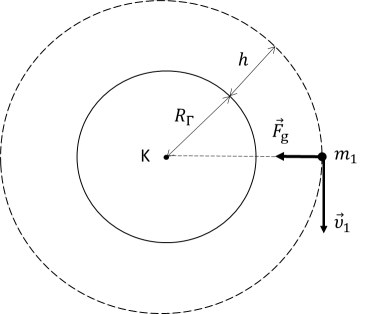
$$F_{g}=F_{k} $$ $$\Rightarrow G\dfrac{M_{Γ}\cdot m_{1}}{(R_{Γ}+h)^{2}}=m_{1}\cdot \dfrac{υ_{1}^{2}}{R_{Γ}+h}$$
Επομένως,
$$υ_{1}=\sqrt{\dfrac{GM_{Γ}}{R_{Γ}+h}}$$ $$ \Rightarrow υ_{1}=\sqrt{\dfrac{g_{0}R_{Γ}^{2}}{\dfrac{16}{9}R_{Γ}}}$$ $$ \Rightarrow υ_{1}=\dfrac{3}{4}\sqrt{g_{0}R_{Γ}}$$
Άρα,
$$υ_{1}=6\cdot 10^{3}\ \dfrac{m}{s}$$
Παρατηρούμε ότι το μέτρο της ταχύτητας περιστροφής του σώματος είναι ανεξάρτητο από τη μάζα του. Το σώμα μάζας \(m_{2}\) περιστρέφεται στο ίδιο ύψος, επομένως:
$$υ_{1}=6\cdot 10^{3}\ \dfrac{m}{s}$$
Μονάδες 6
4.2. Η περίοδος περιστροφής του σώματος μάζας \(m_{1}\) είναι ίση με:
$$Τ_{1}=\dfrac{2π(R_{Γ}+h)}{υ_{1}}$$ $$ \Rightarrow Τ_{1}=\dfrac{32πR_{Γ}}{9υ_{1}}$$ $$ \Rightarrow T_{1}=11915\ s$$
Όμοια,
$$Τ_{2}=T_{1}=11915\ s$$
Μονάδες 6
4. 3. Κατά τη διάρκεια της πλαστικής κρούσης το σύστημα είναι μονωμένο στη διεύθυνση που κινούνται τα σώματα. Έστω \(m_{3}=m_{1}+m_{2}=3m_{1}\), η μάζα του συσσωματώματος.
Εφαρμόζουμε την αρχή διατήρησης της ορμής κατά την πλαστική κρούση.
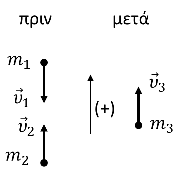
$$Σ\vec{F}_{εξ}=0$$ $$ \Rightarrow \vec{p}_{\text{πριν}}=\vec{p}_{\text{μετά}}$$ $$ \Rightarrow -m_{1}υ_{1}+m_{2}υ_{2}=m_{3}υ_{3}$$ $$ \Rightarrow υ_{3}=\dfrac{υ_{1}}{3}$$
Επομένως,
$$υ_{3}=2\cdot 10^{3}\ \dfrac{m}{s}$$
Μονάδες 6
4. 4. Η ταχύτητα διαφυγής στη θέση που δημιουργείται το συσσωμάτωμα είναι ίση με:
$$υ_{δ}=\sqrt{\dfrac{2GM_{Γ}}{R_{Γ}+h}}$$ $$ \Rightarrow υ_{δ}=\sqrt{\dfrac{2g_{0}R_{Γ}^{2}}{\dfrac{16}{9}R_{Γ}}}$$ $$ \Rightarrow υ_{δ}=\dfrac{3}{4}\sqrt{2g_{0}R_{Γ}}$$ $$ \Rightarrow υ_{δ}=6\sqrt{2}\cdot 10^{3}\ \dfrac{m}{s}$$
Παρατηρούμε ότι, \(υ_{3}<υ_{δ}\), επομένως το συσσωμάτωμα δεν διαφεύγει από το βαρυτικό πεδίο της Γης.
Μονάδες 7
