Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 17682 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική Προσανατολισμού | Τάξη: | Β' Λυκείου | |
| Κωδικός Θέματος: | 16849 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 30-Μαρ-2023 | Ύλη: | 2.5 Η αρχή διατήρησης της ορμής 5.6 Δυναμική ενέργεια πολλών σημειακών φορτίων 5.15 Σύγκριση ηλεκτροστατικού-βαρυτικού πεδίου | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Β' Λυκείου | ||
| Μάθημα: | Φυσική Προσανατολισμού | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 16849 | ||
| Ύλη: | 2.5 Η αρχή διατήρησης της ορμής 5.6 Δυναμική ενέργεια πολλών σημειακών φορτίων 5.15 Σύγκριση ηλεκτροστατικού-βαρυτικού πεδίου | ||
| Τελευταία Ενημέρωση: 30-Μαρ-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Δύο σφαίρες \(Α\) και \(Β\) μικρών διαστάσεων βρίσκονται πάνω σε λείο οριζόντιο δάπεδο κατασκευασμένο από κάποιο μονωτικό υλικό και έχουν μάζες \(m_{A}= 1\ g\) και \(m_{B}= 2\ g\) αντίστοιχα. Οι σφαίρες φέρουν ηλεκτρικά φορτία \(Q_{A}= 0,1\ μC\) και \(Q_{Β}= 0,2\ μC\). Κρατάμε ακίνητες τις σφαίρες σε απόσταση \(x= 2\ cm\) και κάποια στιγμή αφήνουμε ελεύθερη την \(Α\) ενώ τη \(Β\) συνεχίζουμε να την κρατάμε ακίνητη.
Να υπολογίσετε:
4.1. Το μέτρο της επιτάχυνσης της σφαίρας \(Α\), μόλις αυτή αφήνεται ελεύθερη.
Μονάδες 5
4.2. Το μέτρο της ταχύτητας της σφαίρας \(Α\), όταν απέχει απόσταση \(2x\) από την \(Β\).
Μονάδες 7
Επαναφέρουμε τις σφαίρες στην αρχική τους θέση, δηλαδή σε απόσταση \(x\) και στη συνέχεια τις αφήνουμε ταυτόχρονα ελεύθερες και τις δύο. Τη χρονική στιγμή που αυτές απέχουν απόσταση \(2x\) να υπολογίσετε:
4.3. Το μέτρο της επιτάχυνσης της κάθε σφαίρας.
Μονάδες 5
4.4. Το μέτρο της ταχύτητας της κάθε σφαίρας.
Μονάδες 8
Δίνεται \(k_{c}= 9 \cdot 10^{9}\ N\cdot m^{2}/C^{2}\). Η αντίσταση του αέρα και οι βαρυτικές αλληλεπιδράσεις θεωρούνται αμελητέες.
ΘΕΜΑ 4
4.1.
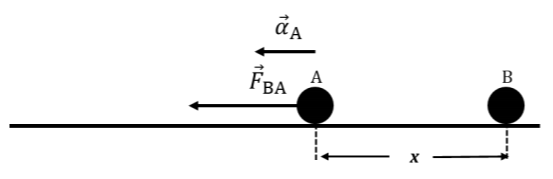
Υπολογίζουμε το μέτρο της δύναμης Coulomb που δέχεται η φορτισμένη σφαίρα \(Α\) από τη φορτισμένη σφαίρα \(Β\):
$$F_{ΒΑ}=k_{C}\dfrac{|q_{A}|\cdot |q_{B}|}{x^{2}}$$ $$=9 \cdot 10^{9}\ \dfrac{N\cdot m^{2}}{C^{2}}\cdot \dfrac{10^{-7}\ C\cdot 2\cdot 10^{-7}\ C}{(2\cdot 10^{-2}\ m)^{2}} $$ $$\Rightarrow F_{ΒΑ}=0,45\ N$$
Υπολογίζουμε το μέτρο της επιτάχυνσης της σφαίρας \(Α\) εφαρμόζοντας τον 2ο νόμο του Νεύτωνα:
$$F_{ΒΑ}=m_{A}\cdot a_{A} $$ $$\Rightarrow a_{A}=\dfrac{F_{ΒΑ}}{m_{A}}=\dfrac{0,45\ Ν}{10^{-3}\ kg}$$ $$\Rightarrow a_{A}=450\ \dfrac{m}{s^{2}}$$
Μονάδες 3+2=5
4.2.
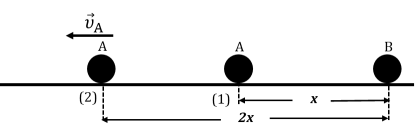
Καθώς η δύναμη Coulomb είναι συντηρητική δύναμη, ισχύει η Αρχή Διατήρησης της Μηχανικής Ενέργειας.
Μονάδες 2
Από τη θέση \((1)\) μέχρι τη θέση \((2)\) έχουμε:
$$E_{\text{ΜΗΧ_1}}=E_{\text{ΜΗΧ_2}} $$ $$\Rightarrow Κ_{1}+U_{1}=Κ_{2}+U_{2}$$ $$\Rightarrow 0+k_{C}\dfrac{q_{A}\cdot q_{B}}{x}=k_{C}\dfrac{q_{A}\cdot q_{B}}{2\cdot x}+\dfrac{1}{2}\cdot m_{A}\cdot υ_{Α}^{2} $$ $$\Rightarrow k_{C}\dfrac{q_{A}\cdot q_{B}}{2\cdot x}=\dfrac{1}{2}\cdot m_{A}\cdot υ_{Α}^{2}$$ $$\Rightarrow υ_{Α}=\sqrt{k_{C}\dfrac{q_{A}\cdot q_{B}}{x\cdot m_{A}}}$$ $$\Rightarrow υ_{Α}=\sqrt{9 \cdot 10^{9}\ \dfrac{N\cdot m^{2}}{C^{2}}\cdot \dfrac{10^{-7}\ C\cdot 2\cdot 10^{-7}\ C}{2\cdot 10^{-2}\ m\cdot 10^{-3}\ kg}}$$ $$\Rightarrow υ_{Α}=3\ \dfrac{m}{s}$$
Μονάδες 5
4.3.
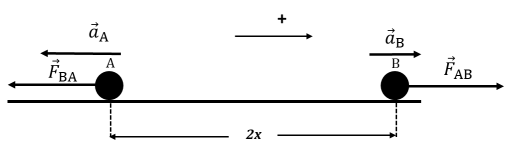
$$F_{ΒΑ}=F_{AB}=k_{C}\dfrac{|q_{A}|\cdot |q_{B}|}{(2\cdot x)^{2}}$$ $$=9 \cdot 10^{9}\ \dfrac{N\cdot m^{2}}{C^{2}}\cdot \dfrac{10^{-7}\ C\cdot 2\cdot 10^{-7}\ C}{(2\cdot 2\cdot 10^{-2}\ m)^{2}}$$ $$\Rightarrow F_{BA}=F_{AB}=\dfrac{9}{80}\ N$$ $$F_{ΒΑ}=m_{A}\cdot a_{A} $$ $$\Rightarrow a_{A}=\dfrac{F_{ΒΑ}}{m_{A}} $$ $$\Rightarrow a_{A}=112,5\ \dfrac{m}{s^{2}}$$ $$F_{AB}=m_{B}\cdot a_{B} $$ $$\Rightarrow a_{B}=\dfrac{F_{AB}}{m_{B}} $$ $$\Rightarrow a_{Β}=56,25\ \dfrac{m}{s^{2}}$$
Μονάδες 3+1+1=5
4.4. Εφαρμόζουμε την Αρχή Διατήρησης της Μηχανικής Ενέργειας από τη θέση, όπου τα δύο φορτισμένα σωματίδια απέχουν μεταξύ τους απόσταση \(x\) μέχρι την θέση, που απέχουν μεταξύ τους απόσταση \(2x\):
$$E_{\text{ΜΗΧ_1}}=E_{\text{ΜΗΧ_2}} $$ $$\Rightarrow Κ_{1}+U_{1}=Κ_{2}+U_{2} $$ $$\Rightarrow 0+k_{C}\dfrac{q_{A}\cdot q_{B}}{x}=k_{C}\dfrac{q_{A}\cdot q_{B}}{2\cdot x}+\dfrac{1}{2}\cdot m_{A}\cdot υ_{Α}^{2}+\dfrac{1}{2}\cdot m_{Β}\cdot υ_{Β}^{2}\ \ \ \ (1)$$
Για το σύστημα των δύο φορτισμένων σωματιδίων ισχύει η Αρχή Διατήρησης της Ορμής:
$$\vec{p}_{\text{ολ,αρχ}}=\vec{p}_{\text{ολ,τελ}} $$ $$\Rightarrow 0=m_{Β}\cdot υ_{Β}-m_{Α}\cdot υ_{Α} $$ $$\Rightarrow 0=2\cdot 10^{-3}\ kg\cdot υ_{Β}-10^{-3}\ kg\cdot υ_{Α} $$ $$\Rightarrow υ_{Α}=2\cdot υ_{Β}\ \ \ \ (2)$$
Μονάδες 4
Από τις σχέσεις \((1)\) και \((2)\) προκύπτει:
$$k_{C}\dfrac{q_{A}\cdot q_{B}}{2\cdot x}=\dfrac{1}{2}υ_{Β}^{2}\cdot (4\cdot m_{Α}+m_{Β}) $$ $$\Rightarrow υ_{Β}=\sqrt{k_{C}\dfrac{q_{A}\cdot q_{B}}{x\cdot (4\cdot m_{A}+m_{Β})}} $$ $$\Rightarrow υ_{Β}=\sqrt{9 \cdot 10^{9}\ \dfrac{N\cdot m^{2}}{C^{2}}\cdot \dfrac{10^{-7}\ C\cdot 2\cdot 10^{-7}\ C}{2\cdot 10^{-2}\ m\cdot 6\cdot 10^{-3}\ kg}} $$ $$\Rightarrow υ_{Β}=\dfrac{\sqrt{6}}{2}\ \dfrac{m}{s}$$
και από τη σχέση \((2)\):
$$υ_{A}=\sqrt{6}\ \dfrac{m}{s}$$
Μονάδες 4