Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 21350 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική Προσανατολισμού | Τάξη: | Γ' Λυκείου | |
| Κωδικός Θέματος: | 23137 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 24-Οκτ-2022 | Ύλη: | 5.3 Κεντρική ελαστική κρούση δύο σφαιρών 1.2 Περιοδικά φαινόμενα 1.3 Απλή αρμονική ταλάντωση | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Γ' Λυκείου | ||
| Μάθημα: | Φυσική Προσανατολισμού | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 23137 | ||
| Ύλη: | 5.3 Κεντρική ελαστική κρούση δύο σφαιρών 1.2 Περιοδικά φαινόμενα 1.3 Απλή αρμονική ταλάντωση | ||
| Τελευταία Ενημέρωση: 24-Οκτ-2022 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Σώμα μάζας \(m_{1}=1\ kg\) αφήνεται να πέσει ελεύθερα από ύψος \(h=5\ m\) πάνω σε δίσκο μάζας \(m_{2}=4\ kg\), ο οποίος ισορροπεί σε κατακόρυφο ιδανικό ελατήριο σταθεράς \(k=100\ \dfrac{N}{m}\). Η κρούση θεωρείται μετωπική και ελαστική και η διάταξη απεικονίζεται στο παρακάτω σχήμα. Αν είναι γνωστό ότι η επιτάχυνση της βαρύτητας είναι \(g=10\ \dfrac{m}{s^{2}}\) και η αντίσταση του αέρα είναι αμελητέα, να βρείτε:
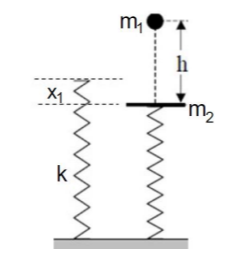
4.1. το μέτρο της ταχύτητας \(υ_{1}\) με την οποία το σώμα προσκρούει στον δίσκο.
Μονάδες 5
4.2. τις ταχύτητες του σώματος και του δίσκου αμέσως μετά την κρούση.
Μονάδες 6
4.3. την μέγιστη δυναμική ενέργεια του ελατηρίου.
Μονάδες 8
4.4. την εξίσωση απομάκρυνσης για την απλή αρμονική ταλάντωση του δίσκου και να την αποδώσετε γραφικά στο χρονικό διάστημα \(0 \le t \le Τ\), όπου \(Τ\) είναι η περίοδος ταλάντωσης του δίσκου. (Να θεωρήσετε θετική φορά προς τα κάτω και ότι αμέσως μετά την κρούση το σώμα απομακρύνεται και δεν συγκρούεται ξανά με τον δίσκο).
Μονάδες 6
ΘΕΜΑ 4
4.1. Το σώμα από την στιγμή που αφήνεται ελεύθερο από ύψος \(h\) πάνω από τον δίσκο και μέχρι να τον συναντήσει εκτελεί ελεύθερη πτώση. Το μέτρο της ταχύτητας με την οποία προσκρούει στον δίσκο μπορεί να υπολογιστεί εφαρμόζοντας τους τύπους της ελεύθερης πτώσης ή με εφαρμογή του θεωρήματος μεταβολής της κινητικής ενέργειας. Με χρήση του δεύτερου τρόπου έχουμε:
$$ΔΚ=W_{ολ}$$ $$\Leftrightarrow Κ_{\text{τελ}}-Κ_{\text{αρχ}}=W_{B}$$ $$\Leftrightarrow \dfrac{m_{1}υ_{1}^{2}}{2}-0=m_{1}gh$$ $$\Leftrightarrow υ_{1}=\sqrt{2gh}=\sqrt{2\cdot 10\cdot 5}\ \dfrac{m}{s}=10\ \dfrac{m}{s}$$
Μονάδες 5
4. 2. Για τον υπολογισμό των ταχυτήτων του σώματος και του δίσκου αμέσως μετά την ελαστική κρούση, θα εφαρμόσουμε τους γνωστούς τύπους από το σχολικό βιβλίο. Η ταχύτητα του σώματος αμέσως μετά την μετωπική ελαστική κρούση είναι:
$$\begin{align} υ_{1}'&=\dfrac{m_{1}-m_{2}}{m_{1}+m_{2}}υ_{1}\\ &=\dfrac{1-4}{1+4}10\ \dfrac{m}{s}\\ &=-6\ \dfrac{m}{s}\end{align}$$
Αντίστοιχα, η ταχύτητα του δίσκου θα είναι:
$$\begin{align} υ_{2}'&=\dfrac{2m_{1}}{m_{1}+m_{2}}υ_{1}\\ &=\dfrac{2\cdot 1}{1+4}10\ \dfrac{m}{s} \\ &=4\ \dfrac{m}{s} \end{align}$$
Μονάδες 6
4. 3. Το ελατήριο θα έχει μέγιστη δυναμική ενέργεια στην θέση της μέγιστης παραμόρφωσης. Αυτή είναι η χαμηλότερη θέση στην οποία θα βρεθεί το ελατήριο κατά την ταλάντωσή του. Στην θέση αυτή η παραμόρφωση του ελατηρίου είναι \(x_{1}+A\), όπου \(x_{1}\) είναι η παραμόρφωση του ελατηρίου στην θέση ισορροπίας του δίσκου και \(Α\) είναι το πλάτος ταλάντωσης του δίσκου. (Στην ανώτερη θέση της ταλάντωσης του δίσκου η παραμόρφωση του ελατηρίου είναι μικρότερη, καθώς είναι \(|x_{1}-A|\).)
Στην θέση ισορροπίας (δείτε το παρακάτω σχήμα) ο δίσκος δέχεται δύο δυνάμεις, το βάρος του \(W_{2}\) και τη δύναμη από το ελατήριο \(F_{ελ}\), οι οποίες έχουν συνισταμένη μηδέν.

Άρα:
$$ΣF=0$$ $$\Leftrightarrow F_{ελ}=W_{2}$$ $$\Leftrightarrow kx_{1}=m_{2}g $$ $$\Leftrightarrow x_{1}=\dfrac{m_{2}g}{k}=\dfrac{4\cdot 10}{100}\ m=0,4\ m$$
Η κυκλική συχνότητα με την οποία γίνεται η ταλάντωση του δίσκου είναι:
$$ω=\sqrt{\dfrac{k}{m_{2}}}=\sqrt{\dfrac{100}{4}}\ \dfrac{rad}{s}=5\ \dfrac{rad}{s}$$
Η ταχύτητα που αποκτά ο δίσκος αμέσως μετά την κρούση είναι η μέγιστη ταχύτητα στην ταλάντωση που εκτελεί, οπότε το πλάτος ταλάντωσης είναι:
$$υ_{2}'=ωΑ \Leftrightarrow Α=\dfrac{υ_{2}'}{ω}=\dfrac{4}{5}\ m=0,8\ m$$
Η μέγιστη δυναμική ενέργεια του ελατηρίου είναι:
$$U_{\text{max,ελ}}=\dfrac{1}{2}k(x_{1}+A)^{2}=\dfrac{1}{2}100(0,4+0,8)^{2}\ J=72\ J$$
Μονάδες 8
4. 4. Η εξίσωση ταλάντωσης έχει γενική μορφή \(x=Aημ(ωt+φ)\). Ο δίσκος την χρονική στιγμή \(t=0\) βρίσκεται στην θέση ισορροπίας (\(d=0\)). Συνεπώς η αρχική φάση είναι \(ημφ=\dfrac{d}{A}=0 \Leftrightarrow φ=0\) γιατί κινείται προς την θετική κατεύθυνση (\(υ>0\)). Άρα η εξίσωση ταλάντωσης είναι:
$$x=0,8ημ(5t) \ \ \ \ \text{(S.I.)}$$
Η περίοδος ταλάντωσης του δίσκου είναι \(Τ=\dfrac{2π}{ω}=0,4π\ s\) και η γραφική παράσταση \(x-t\) φαίνεται στο επόμενο σχήμα.

Μονάδες 6
