Θέμα: 25490

Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!

Επισήμανση θέματος Επισήμανση Προσθήκη στις Εκτυπώσεις Προσθήκη Εκτύπωση Μεμονωμένου Θέματος

Τύπος Σχολείου:	Γενικό Λύκειο	Πηγή: Ι.Ε.Π.	Αναγνώσθηκε: 12596 φορές Επικοινωνία
Μάθημα:	Φυσική Προσανατολισμού	Τάξη:	Γ' Λυκείου
Κωδικός Θέματος:	25490	Θέμα:	2
Τελευταία Ενημέρωση:	14-Νοε-2022	Ύλη:	2.2 Μηχανικά κύματα 7.3 Το φωτοηλεκτρικό φαινόμενο
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida)

Τύπος Σχολείου:	Γενικό Λύκειο
Τάξη:	Γ' Λυκείου
Μάθημα:	Φυσική Προσανατολισμού
Θέμα:	2
Κωδικός Θέματος:	25490
Ύλη:	2.2 Μηχανικά κύματα 7.3 Το φωτοηλεκτρικό φαινόμενο
Τελευταία Ενημέρωση: 14-Νοε-2022
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida)

Αρχείο Εκφώνησης (PDF) Αρχείο Εκφώνησης (DOC)

ΘΕΜΑ 2
2.1. Αρμονικό κύμα διαδίδεται σε γραμμικό ελαστικό μέσο, το οποίο εκτείνεται κατά μήκος θετικού ημιάξονα $Οx$. Η πηγή του κύματος βρίσκεται στη θέση $x_{0}=0$, στο άκρο του ελαστικού μέσου και αρχίζει να ταλαντώνεται τη χρονική στιγμή $t_{0}=0$.

Το διάγραμμα του σχήματος, αποδίδει την απομάκρυνση $y$ από τη θέση ισορροπίας του, σε συνάρτηση με το χρόνο, ενός υλικού σημείου $Α$ του μέσου, του οποίου η θέση ισορροπίας βρίσκεται στη θέση $x_{A}$ του ημιάξονα που ορίσαμε.

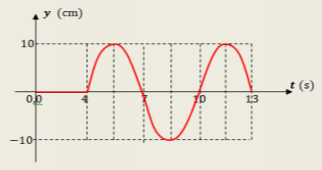
Αν το μήκος κύματος δίνεται $λ=18\ m$, τότε είναι :
(α) $x_{A}=18\ m$
( ) $x_{A}=12\ m$
(γ) $x_{A}=4\ m$

2.1.Α. Να επιλέξετε τη σωστή απάντηση.
Μονάδες 4

2.1. B. Να αιτιολογήσετε την επιλογήσας.
Μονάδες 8

2.2. Στο σχήμα, απεικονίζονται σε κοινό διάγραμμα, οι γραφικές παραστάσεις μέγιστης κινητικής ενέργειας εξερχόμενων ηλεκτρονίων, σε συνάρτηση με τη συχνότητα της προσπίπτουσας ακτινοβολίας, για δύο διαφορετικά πειράματα φωτοηλεκτρικού φαινομένου που πραγματοποιήθηκαν με δύο λυχνίες οι οποίες έχουν διαφορετικό μέταλλο καθόδου.

Πειραματικά προσδιορίσαμε ότι για τις συχνότητες κατωφλίου των δύο λυχνιών ισχύει η σχέση $f_{\text{0,2}}=1,5\cdot f_{\text{0,1}}$. Για μια συχνότητα $f_{1}$ μεγαλύτερη και από τις δύο συχνότητες κατωφλίου, ίδια και στα δύο πειράματα, οι μέγιστες κινητικές ενέργειες ηλεκτρονίων είναι $K_{1}^{max},K_{2}^{max}$ αντίστοιχα.

Αν δίνεται ότι $f_{1}=4\cdot f_{\text{0,1}}$, τότε ισχύει:
(α ) $\dfrac{K_{1}^{max}}{K_{2}^{max}}=1,2$

(β) $\dfrac{K_{1}^{max}}{K_{2}^{max}}=4$

(γ) $\dfrac{K_{1}^{max}}{K_{2}^{max}}=1,5$

2.2.Α. Να επιλέξετε τη σωστή απάντηση.
Μονάδες 4

2.2.B. Να αιτιολογήσετε την επιλογή σας.
Μονάδες 9

Εμφάνιση Απάντησης

Αρχείο Απάντησης (PDF) Αρχείο Απάντησης (DOC)

ΘΕΜΑ 2
2.1.
2.1.Α. Σωστή απάντηση η (β)
Μονάδες 4

2.1.B. Από το διάγραμμα προκύπτει ότι η περίοδος ταλάντωσης είναι $T=6s$, άρα η συχνότητα του αρμονικού κύματος είναι $f=\dfrac{1}{6}Hz$. Το μήκος κύματος δίνεται $λ=18m$. Υπολογίζουμε την ταχύτητα διάδοσης του κύματος στο ελαστικό μέσο:
$υ=λ\cdot f=18\cdot \dfrac{1}{6}\dfrac{m}{s}=3\dfrac{m}{s}$

Από τη γραφική παράσταση φαίνεται ότι το υλικό σημείο $Α$, άρχισε να ταλαντώνεται τη χρονική στιγμή $t_{A}=4s$, και αυτός είναι ο χρόνος που μεσολαβεί από τη στιγμή που άρχισε να ταλαντώνεται το άκρο του μέσου, μέχρι το κύμα να φτάσει στο σημείο $A$.
Άρα υπολογίζουμε: $x_{A}=υ\cdot t_{A}=3\cdot 4\ m=12\ m$
Μονάδες 8

2.2.
2.2.A. Σωστή απάντηση η (α)
Μονάδες 4

2.2.B. Πείραμα (1): Έστω $φ_{1}$ το έργο εξαγωγής ηλεκτρονίου από την επιφάνεια του μετάλλου (1) που χρησιμοποιείται ως κάθοδος στη λυχνία (1). Η συχνότητα κατωφλίου δίνεται $f_{\text{0,1}}$ και ισχύει η σχέση:

$$h\cdot f_{\text{0,1}}-φ_{1}=0,φ_{1}=h\cdot f_{\text{0,1}}(1)$$

Όταν προσπίπτει στην κάθοδο φως με συχνότητα $f_{1}=4\cdot f_{\text{0,1}}$, εξέρχονται ηλεκτρόνια και η μέγιστη κινητική ενέργεια εξερχόμενου ηλεκτρονίου είναι:

$$K_{1}^{max}=h\cdot f_{1}-φ_{1}$$ $$\overset{(1)}{\Rightarrow} K_{1}^{max}=h\cdot 4\cdot f_{\text{0,1}}-h\cdot f_{\text{0,1}}=3\cdot h\cdot f_{\text{0,1}},\ (2)$$

Πείραμα (2): Έστω $φ_{2}$ το έργο εξαγωγής ηλεκτρονίου από την επιφάνεια του μετάλλου (2) που χρησιμοποιείται ως κάθοδος στη λυχνία (2). Η συχνότητα κατωφλίου δίνεται $f_{\text{0,2}}=1,5\cdot f_{\text{0,1}}$ και ισχύει η σχέση:

$$h\cdot f_{\text{0,2}}-φ_{2}=0$$ $$φ_{2}=h\cdot f_{\text{0,2}}=1,5\cdot h\cdot f_{\text{0,1}},\ (3)$$

$$K_{2}^{max}=h\cdot f_{1}-φ_{2}$$ $$\overset{(3)}{\Rightarrow} K_{2}^{max}=h\cdot 4\cdot f_{\text{0,1}}-1,5\cdot h\cdot f_{\text{0,1}}=2,5\cdot h\cdot f_{\text{0,1}},\ (4)$$

Διαιρώντας κατά μέλη τις εξισώσεις $(3)$ και $(4)$, προκύπτει:

$$\dfrac{K_{1}^{max}}{K_{2}^{max}}=\dfrac{3\cdot h\cdot f_{\text{0,1}}}{2,5\cdot h\cdot f_{\text{0,1}}}=\dfrac{3}{2,5}=\dfrac{30}{25}=1,2$$

Μονάδες 9