Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 6433 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Μαθηματικά Προσανατολισμού | Τάξη: | Γ' Λυκείου | |
| Κωδικός Θέματος: | 27321 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 07-Απρ-2023 | Ύλη: | 1.7 Όρια συνάρτησης στο άπειρο 2.2 Παραγωγίσιμες συναρτήσεις - Παράγωγος συνάρτηση 2.3 Κανόνες παραγώγισης 2.7 Τοπικά ακρότατα συνάρτησης 2.9 Ασύμπτωτες - Κανόνες De l’ Hospital 3.5 Η συνάρτηση [ορισμένο ολοκλήρωμα της f από α έως χ] | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Γ' Λυκείου | ||
| Μάθημα: | Μαθηματικά Προσανατολισμού | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 27321 | ||
| Ύλη: | 1.7 Όρια συνάρτησης στο άπειρο 2.2 Παραγωγίσιμες συναρτήσεις - Παράγωγος συνάρτηση 2.3 Κανόνες παραγώγισης 2.7 Τοπικά ακρότατα συνάρτησης 2.9 Ασύμπτωτες - Κανόνες De l’ Hospital 3.5 Η συνάρτηση [ορισμένο ολοκλήρωμα της f από α έως χ] | ||
| Τελευταία Ενημέρωση: 07-Απρ-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Σε μια χώρα, οι επιστήμονες μελέτησαν για μεγάλο χρονικό διάστημα την μεταβολή του πληθυσμού των ψαριών σε έναν ποταμό και δημιούργησαν ένα προσεγγιστικό μαθηματικό μοντέλο που συσχετίζει τον πληθυσμό \(x\) των ψαριών στο τέλος ενός συγκεκριμένου έτους με τον αναμενόμενο πληθυσμό \(y\) των ψαριών στο τέλος της αμέσως επόμενης χρονιάς.
Το μοντέλο εκφράζεται από τη σχέση \(y=f(x)=axe^{-βx}\), \(x∈(0,+∞)\) όπου \(α\), \(β\) θετικές σταθερές, με \(β∈(0,1)\) και \(a∈(1,+∞)\).
(α) Να βρείτε την τιμή του τρέχοντος πληθυσμού \(x\) που μεγιστοποιεί τον πληθυσμό \(y\) των ψαριών το επόμενο έτος σύμφωνα με αυτό το μοντέλο. Ποια είναι αυτή η μέγιστη τιμή του πληθυσμού \(y\) ;
(Μονάδες 9)
(β) Να εξηγήσετε γιατί ένας απεριόριστα μεγάλος πληθυσμός ψαριών δεν θα είναι βιώσιμος την αμέσως επόμενη χρονιά.
(Μονάδες 7)
(γ) Θεωρούμε συνάρτηση \(F\) η οποία είναι μια παράγουσα (αρχική) της συνάρτησης \(f\). Να αποδείξτε ότι: \(F(β)-F(2β)=\dfrac{α}{β^{2}}\cdot \dfrac{2β^{2}+1-(1+β^{2})e^{β^{2}}}{e^{2β^{2}}}\).
(Μονάδες 9)
ΛΥΣΗ
α) Για κάθε \(x>0\), έχουμε:
$$f'(x)=a[(x)'\cdot e^{-βx}+x(e^{-βx})']$$ $$=a[e^{-βx}+x(-βx)'\cdot e^{-βx}]$$ $$=α\cdot e^{-βx}\cdot (1-βx)$$
Έχουμε:
$$f'(x)≥0$$ $$\Leftrightarrow 1-βx≥0$$ $$\Leftrightarrow x≤\dfrac{1}{β}$$
οπότε παίρνουμε τον παρακάτω πίνακα.
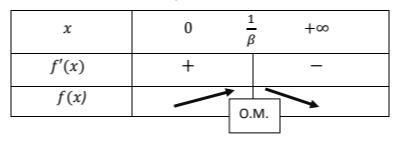
Επομένως όταν ο τρέχων πληθυσμός είναι \(x=\dfrac{1}{β}\), τότε ο πληθυσμός την αμέσως επόμενη χρονιά θα πάρει την μεγαλύτερη δυνατή τιμή, ίση με:
$$f(\dfrac{1}{β})=\dfrac{α}{βe}$$
β) Καθώς θέλουμε να προσεγγίσουμε τον πληθυσμό \(y\) των ψαριών, όταν την αμέσως προηγούμενη χρονιά, ο πληθυσμός είναι απεριόριστα μεγάλος, ζητάμε το:
$$\underset{x\rightarrow +∞}{\lim}{f(x)=}\underset{x\rightarrow +∞}{\lim}α\dfrac{x}{e^{βx}}$$
και παρατηρούμε ότι έχουμε απροσδιοριστία \(\dfrac{+∞}{+∞}\).
Ελέγχουμε αν υπάρχει το:
$$\underset{x\rightarrow +∞}{\lim}\dfrac{(x)'}{(e^{βx})'}=\underset{x\rightarrow +∞}{\lim}\dfrac{1}{βe^{βx}}$$
το οποίο ισούται με μηδέν.
Άρα \(\underset{x\rightarrow +∞}{\lim}{f(x)=}0\) από τον κανόνα DeL’ Hospital, κάτι που σημαίνει ότι αν ο πληθυσμός κάποια χρονιά είναι απεριόριστα μεγάλος, την αμέσως επόμενη χρονιά ο πληθυσμός των ψαριών πρακτικά θα εξαφανιστεί.
γ) Σύμφωνα με το θεμελιώδες θεώρημα του ολοκληρωτικού λογισμού, θα έχουμε:
$$F(β)-F(2β)=\operatorname{\Large\int}_{2β}^{β}f(x)dx$$ $$=α\operatorname{\Large\int}_{2β}^{β}xe^{-βx}dx$$ $$=α\operatorname{\Large\int}_{2β}^{β}x\cdot \left(-\dfrac{1}{β}e^{-βx}\right)'dx$$ $$=α\left\{\left[-\dfrac{x}{β}e^{-βx}\right]\array{β \cr 2β}-\operatorname{\Large\int}_{2β}^{β}\left(x\right)'\cdot \left(-\dfrac{1}{β}e^{-βx}\right)dx\right\}$$ $$=α\left\{-\dfrac{1}{e^{β^{2}}}+\dfrac{2}{e^{2β^{2}}}+\dfrac{1}{β}\operatorname{\Large\int}_{2β}^{β}e^{-βx}dx\right\}$$ $$=α\left\{\dfrac{2-e^{β^{2}}}{e^{2β^{2}}}+\dfrac{1}{β}\left[-\dfrac{1}{β}e^{-βx}\right]\array{β \cr 2β}\right\}$$ $$=α\left[\dfrac{2-e^{β^{2}}}{e^{2β^{2}}}-\dfrac{1}{β^{2}}\left(\dfrac{1}{e^{β^{2}}}-\dfrac{1}{e^{2β^{2}}}\right)\right]$$ $$=α\left(\dfrac{2-e^{β^{2}}}{e^{2β^{2}}}-\dfrac{e^{β^{2}}-1}{β^{2}e^{2β^{2}}}\right)$$ $$=α\dfrac{β^{2}(2-e^{β^{2}})-e^{β^{2}}+1}{β^{2}e^{2β^{2}}}$$ $$=\dfrac{α}{β^{2}}\cdot \dfrac{2β^{2}+1-(1+β^{2})e^{β^{2}}}{e^{2β^{2}}}$$
