Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 9040 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Άλγεβρα | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 33597 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 21-Μαΐ-2023 | Ύλη: | 2.3. Απόλυτη Τιμή Πραγματικού Αριθμού 3.1. Εξισώσεις 1ου Βαθμού 4.1. Ανισώσεις 1ου Βαθμού 6.2. Γραφική Παράσταση Συνάρτησης | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Άλγεβρα | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 33597 | ||
| Ύλη: | 2.3. Απόλυτη Τιμή Πραγματικού Αριθμού 3.1. Εξισώσεις 1ου Βαθμού 4.1. Ανισώσεις 1ου Βαθμού 6.2. Γραφική Παράσταση Συνάρτησης | ||
| Τελευταία Ενημέρωση: 21-Μαΐ-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Στο παρακάτω σχήμα δίνονται οι γραφικές παραστάσεις \(C_{f}\) και \(C_{g}\) των συναρτήσεων \(f\) και \(g\) αντίστοιχα, με:
$$f(x)=|x-2|\ \ \text{και}\ \ g(x)=1\text{ , } x\in \mathbb{R}$$
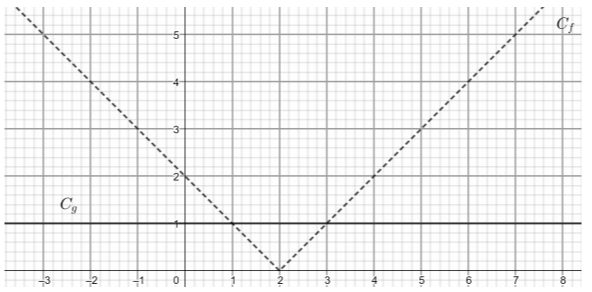
α) Με τη βοήθεια του παραπάνω σχήματος, να βρείτε:
i. τα σημεία τομής των \(C_{f}\) και \(C_{g}\).
(Μονάδες 5)
ii. τις τιμές του \(x\in \mathbb{R}\), για τις οποίες η \(C_{f}\) είναι κάτω από την \(C_{g}\).
(Μονάδες 5)
β) Να επιβεβαιώσετε αλγεβρικά τις απαντήσεις σας στα ερωτήματα αi) και αii).
(Μονάδες 10)
γ) Να βρείτε για ποιες τιμές του \(x\in \mathbb{R}\) η παράσταση \(Α=\dfrac{\sqrt{1-f(x)}}{f(x)}\) ορίζεται στους πραγματικούς αριθμούς.
(Μονάδες 5)
ΛΥΣΗ
α) Από το σχήμα βλέπουμε ότι:
i. τα σημεία τομής των \(C_{f}\) και \(C_{g}\) είναι τα \(Α(1,1)\) και \(Β(3,1)\).
ii. η \(C_{f}\) είναι κάτω από την \(C_{g}\) για \(x\in (1,3)\).
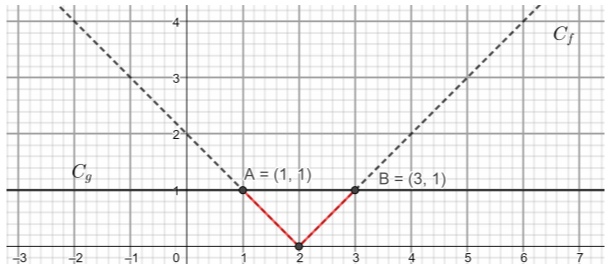
β)
i. Οι τετμημένες των σημείων τομής των \(C_{f}\) και \(C_{g}\) είναι οι λύσεις της εξίσωσης:
$$f(x)=g(x) $$ $$\Leftrightarrow |x-2|=1$$
Έχουμε ισοδύναμα:
$$|x-2|=1$$ $$\Rightarrow \begin{cases} x-2=-1 \\ x-2=1 \end{cases}$$ $$\Rightarrow \begin{cases} x=1 \\ x=3 \end{cases}$$
Έχουμε επίσης \(f(1)=|1-2|=1=g(1)\) και \(f(3)=|3-2|=1=g(3)\), οπότε τα κοινά σημεία των δυο γραφικών παραστάσεων είναι τα \(Α(1,1)\) και \(Β(3,1)\).
ii. Οι τιμές του \(x\in \mathbb{R}\) για τις οποίες η \(C_{f}\) είναι κάτω από την \(C_{g}\) είναι λύσεις της ανίσωσης:
$$f(x) < g(x) $$ $$\Leftrightarrow |x-2| < 1$$
Έχουμε ισοδύναμα:
$$|x-2| < 1 $$ $$\Leftrightarrow -1 < x-2< 1 $$ $$\Leftrightarrow 2-1< x < 2+1 $$ $$\Leftrightarrow 1 < x < 3$$
δηλαδή η \(C_{f}\) είναι κάτω από την \(C_{g}\) για \(x\in (1,3)\).
γ) Η παράσταση \(Α\) ορίζεται στους πραγματικούς αριθμούς αν και μόνο αν:
$$\begin{cases} 1-f(x)\ge 0 \\ \text{και} \\ f(x)\ne 0 \end{cases} $$ $$\Leftrightarrow \begin{cases} f(x)\le 1 \\ \text{και} \\ f(x)\ne 0 \end{cases} $$ $$\Leftrightarrow \begin{cases} |x-2|\le 1 \\ \text{και} \\ |x-2|\ne 0 \end{cases}$$ $$\overset{(βii)}{ \Leftrightarrow } \begin{cases} 1\le x\le 3 \\ \text{και} \\ x\ne 2 \end{cases}$$
Τελικά, η παράσταση \(Α\) ορίζεται στους πραγματικούς αριθμούς για \(x\in [1,2)\cup (2,3]\).