Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 9221 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Άλγεβρα | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 34182 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 01-Νοε-2023 | Ύλη: | 3.3. Εξισώσεις 2ου Βαθμού 4.2. Ανισώσεις 2ου Βαθμού | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Άλγεβρα | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 34182 | ||
| Ύλη: | 3.3. Εξισώσεις 2ου Βαθμού 4.2. Ανισώσεις 2ου Βαθμού | ||
| Τελευταία Ενημέρωση: 01-Νοε-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Στο παρακάτω σχήμα δίνεται τετράγωνο \(ΑΒΓΔ\) πλευράς \(ΑΒ=3\ cm\) και τυχαίο σημείο \(Μ\) που κινείται στη διαγώνιο \(ΒΔ\) εσωτερικά (δηλαδή το \(Μ\) δεν θα ταυτιστεί με τα άκρα της διαγωνίου).
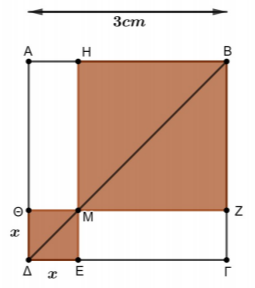
α) Να εκφράσετε το συνολικό εμβαδόν \(Ε\) των σκιασμένων τετραγώνων \(ΗΒΖΜ\) και \(ΘΜΕΔ\) ως συνάρτηση του \(x\) και να βρείτε το πεδίο ορισμού της συνάρτησης \(Ε(x)\).
(Μονάδες 9)
β) Αν το εμβαδόν των σκιασμένων τετραγώνων είναι \(Ε(x)=2x^{2}-6x+9\), να αποδείξετε ότι \(Ε(x)\ge \dfrac{9}{2}\), για κάθε \(x\in (0,3)\).
(Μονάδες 7)
γ) Για ποια θέση του \(Μ\) πάνω στη \(ΒΔ\) το εμβαδόν \(Ε(x)\) γίνεται ελάχιστο, δηλαδή ίσο με \(\dfrac{9}{2}\); Να αιτιολογήσετε την απάντησή σας.
(Μονάδες 9)
ΛΥΣΗ
α) Το τετράγωνο \(ΘΜΕΔ\) έχει πλευρά \(x>0\ \ \ \ (1)\).
Το εμβαδόν του \(Ε_{1}=x^{2}\).
Το τετράγωνο \(ΗΒΖΜ\) έχει πλευρά \((3-x)>0 \Leftrightarrow x<3\ \ \ \ (2)\).
Το εμβαδόν του είναι \(Ε_{2}=(3-x)^{2}\).
Άρα το συνολικό εμβαδόν \(Ε\) ως συνάρτηση του \(x\) είναι:
$$Ε(x)=Ε_{1}+Ε_{2}$$ $$=x^{2}+(3-x)^{2}$$ $$=2x^{2}-6x+9$$
Από \((1)\) και \((2)\), το πεδίο ορισμού της συνάρτησης \(Ε(x)\) είναι \(Α=(0,3)\).
β) Έχουμε:
$$Ε(x)\ge \dfrac{9}{2} $$ $$\Leftrightarrow 2x^{2}-6x+9\ge \dfrac{9}{2} $$ $$\Leftrightarrow 4x^{2}-12x+9\ge 0 $$ $$\Leftrightarrow (2x-3)^{2}\ge 0$$
, που ισχύει για κάθε \(x\in (0,3)\).
γ) ‘Έχουμε:
$$Ε(x)=\dfrac{9}{2}$$ $$\overset{(β)}{ \Leftrightarrow} (2x-3)^{2}=0 $$ $$\Leftrightarrow 2x-3=0 $$ $$\Leftrightarrow x=\dfrac{3}{2}$$
Το εμβαδόν γίνεται ελάχιστο αν και μόνο αν \(x=\dfrac{3}{2}\), δηλαδή αν και μόνο αν το σημείο \(Ε\) είναι μέσο της \(ΔΓ\). Στο \(ΔΒΓ\) τρίγωνο έχουμε:
\(Ε\) μέσο της \(ΔΓ\) και \(ΜΕ \parallel ΒΓ\), οπότε και \(Μ\) θα είναι μέσο της \(ΒΔ\).
