Θέμα: 36683

Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!

Τύπος Σχολείου:	Γενικό Λύκειο	Πηγή: Ι.Ε.Π.	Αναγνώσθηκε: 6990 φορές Επικοινωνία
Μάθημα:	Άλγεβρα	Τάξη:	Α' Λυκείου
Κωδικός Θέματος:	36683	Θέμα:	4
Τελευταία Ενημέρωση:	20-Μαΐ-2023	Ύλη:	3.1. Εξισώσεις 1ου Βαθμού 6.1. Η Έννοια της Συνάρτησης 6.2. Γραφική Παράσταση Συνάρτησης 6.3. Η Συνάρτηση ƒ(x) = αx + β
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida)

Τύπος Σχολείου:	Γενικό Λύκειο
Τάξη:	Α' Λυκείου
Μάθημα:	Άλγεβρα
Θέμα:	4
Κωδικός Θέματος:	36683
Ύλη:	3.1. Εξισώσεις 1ου Βαθμού 6.1. Η Έννοια της Συνάρτησης 6.2. Γραφική Παράσταση Συνάρτησης 6.3. Η Συνάρτηση ƒ(x) = αx + β
Τελευταία Ενημέρωση: 20-Μαΐ-2023
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida)

Αρχείο Εκφώνησης (PDF) Αρχείο Εκφώνησης (DOC)

ΘΕΜΑ 4

Δίνεται η συνάρτηση $f$, με:

$$f(x)=\begin{cases} - x+2,\ \ \text{αν}\ \ x < 0 \\ x+2,\ \ \text{αν}\ \ x \ge 0 \end{cases}$$

α) Να βρείτε το σημείο τομής της γραφικής παράστασης $C_{f}$ της $f$ με τον άξονα $y'y$.
(Μονάδες 3)

β)
i) Να χαράξετε τη $C_{f}$ και την ευθεία $y=3$, και στη συνέχεια να εκτιμήσετε τις συντεταγμένες των σημείων τομής τους.
(Μονάδες 5)

ii) Nα εξετάσετε αν τα σημεία αυτά είναι συμμετρικά ως προς τον άξονα $y'y$. Να αιτιολογήσετε την απάντησή σας.
(Μονάδες 4)

γ)
i) Για ποιες τιμές του πραγματικού αριθμού $α$, η ευθεία $y=α$ τέμνει τη $C_{f}$ σε δυο σημεία; Να αιτιολογήσετε την απάντησή σας.
(Μονάδες 5)

ii) Για τις τιμές του $α$ που βρήκατε στο ερώτημα (γi), να προσδιορίσετε αλγεβρικά τα σημεία τομής της $C_{f}$ με την ευθεία $y=α$ και να εξετάσετε αν ισχύουν τα συμπεράσματα του ερωτήματος (βii), αιτιολογώντας τον ισχυρισμό σας.
(Μονάδες 8)

Εμφάνιση Απάντησης

Αρχείο Απάντησης (PDF) Αρχείο Απάντησης (DOC)

ΛΥΣΗ

α) Αντικαθιστούμε στον τύπο της $f$, και συγκεκριμένα στον κλάδο $x+2$ όπου $x=0$ και βρίσκουμε: $f(0)=0+2=2$.

Άρα η $C_{f}$ τέμνει τον άξονα $y'y$ στο σημείο $Μ(0,2)$.

β)
i)
Για $x=-1$ είναι: $f(-1)=-(-1)+2=1+2=3$.
Για $x=-2$ είναι: $f(-2)=-(-2)+2=2+2=4$.
Άρα η ημιευθεία $y=-x+2$ διέρχεται από τα σημεία $Α(-1,3)$ και $Β(-2,4)$.

Για $x=1$ είναι: $f(1)=1+2=3$.
Για $x=2$ είναι: $f(2)=2+2=4$.
Άρα η ημιευθεία $y=x+2$ διέρχεται από τα σημεία $Γ(1,3)$ και $Δ(2,4)$.

Η ευθεία $y=3$ είναι μια ευθεία παράλληλη στον άξονα $x'x$ και διέρχεται από το σημείο $Ε(0,3)$.

Η γραφική παράσταση $C_{f}$ και η ευθεία $y=3$ φαίνονται στο παρακάτω σχήμα.

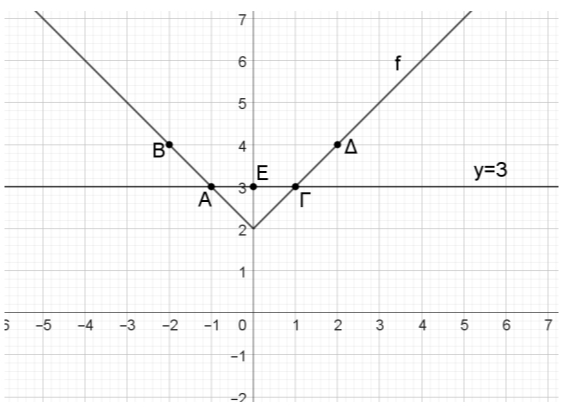
Από τη γραφική παράσταση διαπιστώνουμε ότι τα σημεία τομής της $C_{f}$ με την ευθεία $y=3$ είναι τα $Α(-1,3)$ και $Γ(1,3)$.

ii) Τα σημεία $Α(-1,3)$ και $Γ(1,3)$ έχουν αντίθετες τετμημένες και ίσες τεταγμένες. Άρα είναι συμμετρικά ως προς τον άξονα $y'y$.

γ)
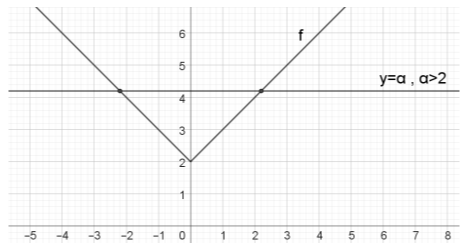
i) Η ευθεία $y=α$ είναι μια ευθεία παράλληλη στον άξονα $x'x$ και διέρχεται από το σημείο $(0,α)$. Όπως διαπιστώνουμε και από τα παρακάτω σχήματα, η ευθεία $y=α$ τέμνει τη $C_{f}$ σε δύο σημεία αν καιμόνο αν $α>2$.

ii) Ο τύπος της $f$ γράφεται: $f(x)=|x|+2$, $x\in \mathbb{R}$.

Οι τετμημένες των σημείων τομής της $C_{f}$ με την ευθεία $y=α$ είναι οι λύσεις της εξίσωσης:

$$f(x)=α $$ $$\Leftrightarrow |x|+2=α $$ $$\Leftrightarrow |x|=α-2$$

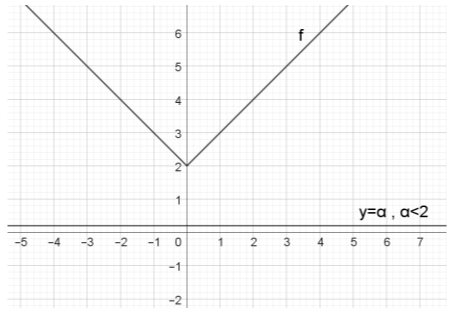
Αν $α<2 \Leftrightarrow α-2 < 0$ η εξίσωση $|x|=α-2$ είναι αδύνατη και επομένως η $C_{f}$ με την ευθεία $y=α$ δεν έχουν κοινά σημεία, όπως φαίνεται και στο τελευταίο σχήμα.

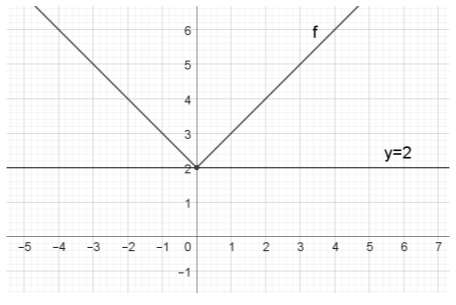
Αν $α=2$ η εξίσωση $|x|=α-2 \Leftrightarrow |x|=0 \Leftrightarrow x=0$ και επομένως η $C_{f}$ με την ευθεία $y=2$ έχουν ένα κοινό σημείο το $(0,2)$ όπως φαίνεται και στο προτελευταίο σχήμα.

Αν $α>2$ η εξίσωση $|x|=α-2 \Leftrightarrow x=α-2$ ή $x=-α+2$ δηλαδή δύο λύσεις διαφορετικές και επομένως η $C_{f}$ με την ευθεία $y=α$ έχουν δύο κοινά σημεία τα $(α-2, α)$ και $(-α+2, α)$ όπως φαίνεται και στα δύο πρώτα σχήματα.