Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 19843 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 7975 | Θέμα: | 2 | |
| Τελευταία Ενημέρωση: | 29-Απρ-2024 | Ύλη: | Χωρίς Αντιστοίχιση Ύλης | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Φυσική | ||
| Θέμα: | 2 | ||
| Κωδικός Θέματος: | 7975 | ||
| Ύλη: | Χωρίς Αντιστοίχιση Ύλης | ||
| Τελευταία Ενημέρωση: 29-Απρ-2024 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ Β
Β1. Μοτοσικλετιστής βρίσκεται ακίνητος σε ένα σημείο \(Α\). Τη χρονική στιγμή \(t = 0s\) ξεκινά και κινείται ευθύγραμμα με σταθερή επιτάχυνση.
Α) Να επιλέξετε την σωστή απάντηση.
Αν ο μοτοσικλετιστής βρίσκεται τη χρονική στιγμή \(t_{1}\) σε απόσταση \(10 m\) από το σημείο \(Α\), τότε τη χρονική στιγμή \(2t_1\) θα βρίσκεται σε απόσταση από το \(Α\) ίση με:
α) \(20\ m\)
β) \(40\ m\)
γ) \(80\ m\)
Μονάδες 4
Β) Να δικαιολογήσετε την επιλογή σας.
Μονάδες 8
Β2. Κιβώτιο βρίσκεται αρχικά ακίνητο σε λείο οριζόντιο δάπεδο στη θέση \(x_{0} = 0 m\), ενός οριζόντιου άξονα \(x'x\). Τη χρονική στιγμή \(t = 0 s\) ένας εργάτης σπρώχνει και αρχίζει να κινεί το κιβώτιο ασκώντας σε αυτό σταθερή οριζόντια δύναμη μέτρου \(F\).
A) Αν με \(x\) συμβολίσουμε τη θέση του κιβωτίου και με \(K\) την κινητική ενέργεια του κιβωτίου στη θέση αυτή, να προσδιορίσετε τη σχέση της κινητικής ενέργειας σε συνάρτηση με τη θέση του κιβωτίου.
Μονάδες 7
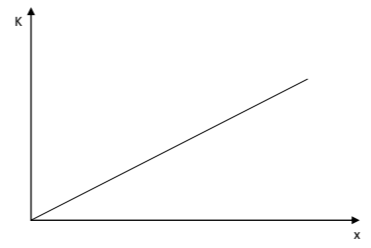
B) Να κατασκευάσετε τη γραφική παράσταση της κινητικής ενέργειας \(Κ\), σε συνάρτηση με τη θέση \(x\).
Μονάδες 6
ΘΕΜΑ Β
Β1. Σωστή η απάντηση (β)
Ενδεικτική Αιτιολόγηση
Επειδή η επιτάχυνση \(α\) είναι σταθερή ισχύει:
$$x_1=\dfrac{1}{2}α\cdot t^{2}\ \ \ \ (1)$$
$$x_2=\dfrac{1}{2}α\cdot (2t)^{2}$$ $$\Rightarrow x_2=\dfrac{1}{2}α\cdot 4t^{2}$$ $$\Rightarrow x_2=4x_1$$ $$\Rightarrow x_2=40\ m \ \ \ \ (2)$$
Β2.
Εφαρμόζουμε το Θεώρημα Μεταβολής Κινητικής Ενέργειας -Έργου για την κίνηση του κιβωτίου μεταξύ των θέσεων \(x_{0}\) και \(x\).
Είναι: \(K-K_{0}=W\) ή \(K=F\cdot x\)
Επειδή \(F=σταθ.\) προκύπτει ότι η γραφική παράσταση \(Κ=f(x)\) είναι μια ευθεία γραμμή που διέρχεται από την αρχή των αξόνων.