Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 4609 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 8045 | Θέμα: | 2 | |
| Τελευταία Ενημέρωση: | 24-Νοε-2021 | Ύλη: | Χωρίς Αντιστοίχιση Ύλης | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Φυσική | ||
| Θέμα: | 2 | ||
| Κωδικός Θέματος: | 8045 | ||
| Ύλη: | Χωρίς Αντιστοίχιση Ύλης | ||
| Τελευταία Ενημέρωση: 24-Νοε-2021 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
Β ΘΕΜΑ
Β1. Ένας μικρός κύβος βρίσκεται ακίνητος πάνω σε λείο οριζόντιο δάπεδο. Τη στιγμή \(t = 0 s\) αρχίζει να ασκείται στον κύβο οριζόντια δύναμη \(\vec{F}\) σταθερής κατεύθυνσης της οποίας το μέτρο μεταβάλλεται με το χρόνο όπως παριστάνεται στο διάγραμμα.

Α) Να επιλέξετε την σωστή απάντηση:
Η επιτάχυνση με την οποία θα κινηθεί ο κύβος θα έχει
α) σταθερό μέτρο και μεταβαλλόμενη κατεύθυνση.
β) μέτρο που αυξάνεται με το χρόνο και σταθερή κατεύθυνση.
γ) μέτρο που μειώνεται με το χρόνο και σταθερή κατεύθυνση.
Μονάδες 4
Β) Να δικαιολογήσετε την επιλογή σας.
Μονάδες 8
Β2. Θέλουμε να διερευνήσουμε πότε μια δύναμη παράγει μεγαλύτερο έργο σε ένα χρονικό διάστημα \(Δt\), όταν ασκείται μόνη της σε ένα σώμα ή όταν ασκείται ταυτόχρονα με μια άλλη δύναμη. Για το λόγο αυτό, θα διερευνήσουμε δύο περιπτώσεις άσκησης δυνάμεων σε ένα κιβώτιο που είναι ακίνητο σε λείο οριζόντιο δάπεδο.
Περίπτωση Ι: Τη στιγμή \(t_0 = 0 s\) αρχίζει να ασκείται σταθερή οριζόντια δύναμη \(\vec{F_1}\).
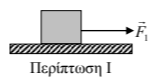
Περίπτωση ΙΙ: Τη στιγμή \(t_0 = 0 s\) αρχίζει να ασκείται η δύναμη \(\vec{F_1}\) (που ασκείται και στην περίπτωση Ι) ταυτόχρονα με μια άλλη ομόρροπη σταθερή οριζόντια δύναμη \(\vec{F_2}\).

Α) Να επιλέξετε την σωστή απάντηση.
Ονομάζουμε \(W_{F_1(I)}\) το έργο που παράγει η \(\vec{F_1}\) σε χρονικό διάστημα \(Δt=t-t_0\) στην περίπτωση (Ι) και \(W_{F_1(ΙI)}\) το έργο που παράγει η \(\vec{F_1}\) ίδιο χρονικό διάστημα \(Δt\) στην περίπτωση (ΙΙ).
Θα ισχύει:
(α) \(W_{F_1(I)} < W_{F_1(IΙ)}\)
(β) \(W_{F_1(I)} > W_{F_1(IΙ)}\)
(γ) \(W_{F_1(I)} = W_{F_1(IΙ)}\)
Μονάδες 4
Β) Να δικαιολογήσετε την επιλογή σας.
Μονάδες 9
Β1. Σωστή απάντηση η (β)
Ενδεικτική Αιτιολόγηση
Σύμφωνα με τον 2ο Νόμο του Νεύτωνα
$$\vec{α}=\dfrac{\vec{F}}{m}$$
Επομένως η επιτάχυνση θα μεταβάλλεται όπως η δύναμη.
Β2. Σωστή απάντηση η (α).
Ενδεικτική Αιτιολόγηση
Στην περίπτωση (Ι) η μετατόπιση του σώματος στο χρονικό διάστημα \(Δt\) είναι:
$$Δx_{(Ι)} = \dfrac{1}{2} α \cdot (Δt)^2$$
Στην περίπτωση (ΙΙ) η μετατόπιση στο ίδιο χρονικό διάστημα θα είναι:
$$Δx_{(II)} =\dfrac{1}{2} α' \cdot (Δt)^2$$
Από το 2ο Νόμο του Νεύτωνα:
$$α =\dfrac{F_1}{m} \text{ και } α'=\dfrac{{F_1}+{F_2}}{m}$$
Οπότε: \(α < α'\), άρα και \(Δx_{(I)} < Δx_{(IΙ)}, \ (1)\)
Αλλά ισχύουν:
$$W_{F_1(I)} = F_1 \cdot Δx_{(I)} \text{ και } W_{F_1(II)} = F_1 \cdot Δx_{(II)}, \ (2)$$
Από τις σχέσεις (1) και (2) συμπεραίνουμε ότι:
$$W_{F_1(I)} \lt W_{F_1(II)}$$
