Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 29290 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 11623 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 26-Μαρ-2025 | Ύλη: | Χωρίς Αντιστοίχιση Ύλης | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Φυσική | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 11623 | ||
| Ύλη: | Χωρίς Αντιστοίχιση Ύλης | ||
| Τελευταία Ενημέρωση: 26-Μαρ-2025 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ Δ
Σε ένα κιβώτιο μάζας \(1\ kg\) που κινείται ευθύγραμμα σε οριζόντιο δρόμο, ασκείται σταθερή οριζόντια δύναμη \(F\), όπως φαίνεται στο σχήμα. Το κιβώτιο κινείται με σταθερή ταχύτητα μέτρου \(10\ m/s\). Ο συντελεστής τριβής ολίσθησης μεταξύ του κιβωτίου και του δρόμου είναι \(μ = 0,2\).
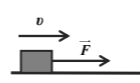
Τη χρονική στιγμή \(t = 0\ s\) ένας μαθητής ξεκινά να παρατηρεί την κίνηση του κιβωτίου. Να υπολογίσετε:
Δ1) το μέτρο της δύναμης \(F\)
Μονάδες 6
Δ2) το έργο της δύναμης \(F\), από τη χρονική στιγμή \(t = 0\), μέχρι τη στιγμή που το χρονόμετρο του μαθητή δείχνει \(t_1 = 5\ s\).
Μονάδες 6
Τη χρονική στιγμή \(t_1\), καταργείται η δύναμη \(F\). Να υπολογίσετε :
Δ3) τη συνολική μετατόπιση του κιβωτίου από τη χρονική στιγμή \(t = 0\), μέχρι τη στιγμή που σταμάτησε να κινείται.
Μονάδες 7
Δ4) το έργο της τριβής, από την χρονική στιγμή \(t_1\) μέχρι τη χρονική στιγμή που το κιβώτιο σταμάτησε να κινείται.
Μονάδες 6
Θεωρήστε την επιτάχυνση της βαρύτητας ίση με \(g = 10\ m/s^2\) και ότι η αντίσταση του αέρα είναι αμελητέα.
Ενδεικτική Λύση
Δ1) Το κιβώτιο \(Α\) εκτελεί ευθύγραμμη ομαλή κίνηση και από τον 1ο νόμο του Νεύτωνα έχουμε :
$$ΣF=0$$
Άρα η δύναμη \(F\) είναι ίση κατά μέτρο με την τριβή ολίσθησης που εμφανίζεται μεταξύ κιβωτίου και δρόμου.
$$Τ =μ \cdot N = μ \cdot B = μ \cdot m \cdot g$$
Οπότε και \(F = 2\ N\).
Δ2) Το κιβώτιο για το χρονικό διάστημα από \(t = 0\ s\) μέχρι \(t_1 = 5\ s\) κινείται με σταθερή ταχύτητα, οπότε μετατοπίζεται κατά \(Δx_1 =50\ m\). Άρα το έργο της δύναμης \(F\) υπολογίζεται από τον τύπο:
$$W_F = F \cdot Δx_1$$ $$\Rightarrow W_F = 100\ J$$
Δ3) Όταν παύσει να ασκείται η δύναμη \(F\), το κιβώτιο θα κινηθεί ευθύγραμμα υπό την επίδραση της τριβής ολίσθησης, μέχρι να ακινητοποιηθεί.
Με βάση το 2ο νόμο του Νεύτωνα \(ΣF=m\cdot α\), η επιβράδυνση που θα έχει το σώμα τότε θα είναι:
$$α = 2\ \dfrac{m}{s^2}$$
Η εξίσωση της ταχύτητας για την επιβραδυνόμενη αυτή κίνηση θα είναι:
$$υ_{τελ}=υ-αt$$
και τελικά ο χρόνος κίνησης για το διάστημα από \(t_1\) μέχρι να ακινητοποιηθεί υπολογίζεται σε \(5\ s\).
Άρα κάνει δύο κινήσεις:
1η Κίνηση: αρχικά Ε.Ο.Κ. για \(5\ s\) (όπου μετατοπίζεται κατά \(50\ m\)) και
2η Κίνηση: στη συνέχεια επιβραδυνόμενη κίνηση για άλλα \(5\ s\).
Η μετατόπιση σε αυτό το χρόνο (\(Δt_2=t_2-t_1\)) προκύπτει:
$$Δ{x_2} = υ \cdot (Δt_2) -\dfrac{1}{2}α\cdot (Δt_2)^2= 25\ m$$
Άρα η συνολική μετατόπιση για όσο κινείται το κιβώτιο είναι: \(75\ m\).
Δ4) Το έργο της τριβής είναι:
$$W_T = -T \cdot Δx_2$$
Επομένως για τα \(25\) μέτρα μέχρι να σταματήσει να κινείται, το έργο της τριβής θα είναι:
$$W_T = -50\ J$$
