ΘΕΜΑ Δ

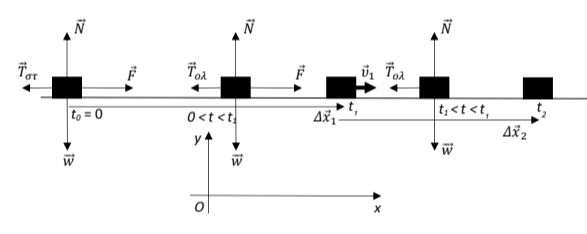
Δ1. Τη χρονική στιγμή $t_0=0$ στο σώμα ασκείται το γήινο βάρος του $\overrightarrow{w}$, η δύναμη $\overrightarrow{F}$ και η δύναμη από το δάπεδο, η οποία αναλύεται στην $\overrightarrow{N}$ και στην στατική τριβή ${\overrightarrow{T}}_{\sigma \tau }$. Το σώμα θα αρχίσει να κινείται τη χρονική στιγμή $t_0=0$ αν $F>T_{o\rho }$, όπου $F$ το μέτρο της δύναμης $\overrightarrow{F}$ και $T_{o\rho }$ το μέτρο της οριακής (μέγιστης στατικής) τριβής. Τη χρονική στιγμή $t_0=0$ το σώμα είναι ακίνητο, οπότε σύμφωνα με τον 1ο νόμο του Newton:

$$\sum \overrightarrow{F_y}=\overrightarrow{0}$$ $$\Rightarrow N=w$$ $$\Rightarrow N=m\cdot g$$ $$\Rightarrow N=10N$$

Από τον νόμο της οριακής τριβής:

$${{\rm T}}_{o\rho }={\mu }_{o\rho }\cdot {\rm N}$$ $$\Rightarrow {{\rm T}}_{o\rho }=5{\rm N}$$

Επειδή:

$$F=10N>5N=T_{o\rho }$$

το σώμα θα αρχίσει να κινείται τη χρονική στιγμή $t_0=0$.
Μονάδες 5

Δ2.
Δ.2.1. Από τον νόμο της τριβής ολίσθησης:

$${{\rm T}}_{o\lambda }={\mu }_{o\lambda }\cdot {\rm N}$$ $$\Rightarrow {{\rm T}}_{o\lambda }=4{\rm N}$$

καθ’ όλη τη διάρκεια της κίνησης (Μονάδες 2).

Στο χρονικό διάστημα ($0$  ,  $t_1=10s$), από τον Θεμελιώδη νόμο της Μηχανικής, ισχύει:

$$\sum {\overrightarrow{F}}_{x,1}=m\cdot {\overrightarrow{a}}_1$$ $$\Rightarrow F-T_{o\lambda }=m\cdot a_1$$ $$\Rightarrow a_1={\displaystyle \frac{F-T_{o\lambda }}{m}}$$ $$\Rightarrow a_1=6{\displaystyle \frac{m}{s^2}}$$

(Μονάδες 4)

Τη χρονική στιγμή $t_1=10s$ ισχύουν:

$$\left\{\begin{array}{c}{\upsilon }_1={\upsilon }_0+{\alpha }_1\cdot t_1\text{,}{\upsilon }_1=60{\displaystyle \frac{m}{s}}\text{(μονάδες 2)}\\ \Delta x_1={\upsilon }_0\cdot t_1+{\displaystyle \frac{1}{2}}\cdot a_1\cdot t_1^2=300m\text{(μονάδες 2)}\end{array}\right\}$$

Στο χρονικό διάστημα ($t_1=10s$  , $t_2$), από την αρχή διατήρησης της ενέργειας, ισχύει:

$$\Delta {\rm K}=W_{{\overrightarrow{T}}_{o\lambda }}$$ $$\Rightarrow {{\rm K}}_2-{{\rm K}}_1=-{{\rm T}}_{o\lambda }\cdot \Delta x_2$$ $$\Rightarrow \Delta x_2=-{\displaystyle \frac{K_2-K_1}{{{\rm T}}_{o\lambda }}}$$ $$\Rightarrow \Delta x_2=-{\displaystyle \frac{0-{\displaystyle \frac{1}{2}}\cdot m\cdot {\upsilon }_1^2}{{{\rm T}}_{o\lambda }}}$$ $$\Rightarrow \Delta x_2=450m$$

(Μονάδες 4)

Τελικά:

$$\Delta x_{o\lambda }=\Delta x_1+\Delta x_2=750m$$

(Μονάδα 1).

Μονάδες 15

Δ.2.2. Για τη συνολική θερμότητα που εκλύθηκε στο περιβάλλον ισχύει:

$$Q=\left|W_{{\overrightarrow{T}}_{o\lambda }}\right|={{\rm T}}_{o\lambda }\cdot (\Delta x_1+\Delta x_2)$$ $$\Rightarrow Q=3000J$$

Μονάδες 5