Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 17371 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 13588 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 24-Μαρ-2023 | Ύλη: | 1.1 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ 1.1.8 Η έννοια της επιτάχυνσης στην ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 1.1.9. Οι εξισώσεις προσδιορισμού της ταχύτητας και της θέσης ενός κινητού στην ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ 1.2.1 Η έννοια της δύναμης 1.2.4 Ο δεύτερος νόμος του Νεύτωνα ή Θεμελιώδης νόμος της Μηχανικής 1.2.7 Η ελεύθερη πτώση των σωμάτων 2.1 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ 2.1.1 Η έννοια του έργου | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Φυσική | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 13588 | ||
| Ύλη: | 1.1 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ 1.1.8 Η έννοια της επιτάχυνσης στην ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 1.1.9. Οι εξισώσεις προσδιορισμού της ταχύτητας και της θέσης ενός κινητού στην ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ 1.2.1 Η έννοια της δύναμης 1.2.4 Ο δεύτερος νόμος του Νεύτωνα ή Θεμελιώδης νόμος της Μηχανικής 1.2.7 Η ελεύθερη πτώση των σωμάτων 2.1 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ 2.1.1 Η έννοια του έργου | ||
| Τελευταία Ενημέρωση: 24-Μαρ-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
Θέμα 4ο
Πειραματική διάταξη περιλαμβάνει μια σφαίρα μάζας \(m = 1kg\) που αφήνεται να πέσει από ύψος \(h\) (από το έδαφος), απέναντι από ακίνητη ψηφιακή φωτογραφική μηχανή που είναι προ ρυθμισμένη να παίρνει λήψεις ανά συγκεκριμένα χρονικά διαστήματα \(Δ_t = 0,1 s\).
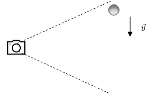
Στη συνέχεια μελετώντας τις φωτογραφίες μπορεί κανείς να υπολογίσει τα φυσικά μεγέθη που σχετίζονται με το φαινόμενο που εξελίχθηκε μπροστά από τη φωτ. μηχανή. Δίνεται: \(g = 10 \ m/s2\)
4.1) Αν συγκρίνουμε την 1η φωτογραφία (\(t = 0\), η στιγμή που αφήνεται η σφαίρα) και την 6η φωτογραφία μετράμε ότι η σφαίρα έχει μετατοπιστεί \(1 \ m\). Μπορούμε να επιβεβαιώσουμε αν η σφαίρα κάνει ελεύθερη πτώση ή όχι; Να αιτιολογήσετε την απάντηση σας.
4.2) Αν θεωρήσουμε ότι όλες οι δυνάμεις που ασκούνται στη σφαίρα είναι σταθερού μέτρου, να υπολογίσετε πόσο επιπλέον θα έχει μετατοπιστεί η σφαίρα στην 7η φωτογραφία.
4.3) Να υπολογίσετε τα μέτρα των δυνάμεων που ασκούνται στη σφαίρα.
4.4) Αν η σφαίρα φτάνει στο έδαφος ακριβώς τη στιγμή που η φωτ. μηχανή βγάζει την 11η φωτογραφία, να υπολογίσετε την αρχική βαρυτική δυναμική ενέργεια της σφαίρας ως προς το έδαφος και την τελική κινητική της ενέργεια ακριβώς πριν ακουμπήσει στο έδαφος.
(Μονάδες 6+6+5+8)
Ενδεικτική Λύση
4.1) Τα χρονικά διαστήματα στα οποία η φωτογραφική μηχανή λάμβανε λήψεις όσο έπεφτε η σφαίρα φαίνονται στον πιο κάτω πίνακα:
| Λήψεις | 1η | 2η | 3η | 4η | 5η | 6η | 7η | 8η | 9η | 10η | 11η |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Χρόνος (s) | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
Συνεπώς από την 1η έως την 6η λήψη έχουν μεσολαβήσει \(0,5 \ s\) Η σφαίρα κάνει ευθύγραμμη ομαλά επιταχυνόμενη κίνηση χωρίς αρχική ταχύτητα, οπότε μπορούμε να υπολογίσουμε την επιτάχυνση της σφαίρας:
$$\begin{align}𝛥_𝑥&=\frac{1}{2}\cdot 𝛼\cdot 𝑡^2\\ 𝛼&=\frac{2\cdot 𝛥_𝑥}{𝑡^2}\\ 𝛼&=8\frac{𝑚}{𝑠^2}\end{align}$$
άρα η σφαίρα δεν κάνει ελεύθερη πτώση.(Μονάδες 6)
4.2) Το σώμα από την 6η φωτογραφία στην 7η θα έχει μετακινηθεί κατά \(𝛥_𝑦\)
$$𝛥_𝑦=\frac{1}{2}\cdot 𝛼\cdot 𝑡^2_7−\frac{1}{2}\cdot 𝛼\cdot 𝑡^2_6=(\frac{1}{2}\cdot 8\cdot 0,6^2−\frac{1}{2}\cdot 8\cdot 0,5^2)𝑚=0,44 \ 𝑚$$
(Μονάδες 6)
4.3) Αν το σώμα έκανε ελεύθερη πτώση θα κινούνταν με την επιτάχυνση της βαρύτητας. Αυτό όμως δεν ισχύει συνεπώς πέρα από το βάρος ασκείται και η αντίσταση του αέρα. Σύμφωνα με το 2ο νόμο του Newton:
$$𝑚\cdot 𝑔−𝐹_𝐴=𝑚\cdot 𝛼$$
Το βάρος του σώματος είναι \(𝑚\cdot 𝑔=10 \ 𝛮\) , συνεπώς η αντίσταση του αέρα θα είναι:
$$\begin{align}𝐹_𝐴&=𝑚\cdot 𝑔−𝑚\cdot 𝛼\\ 𝐹_𝐴&=10−8 𝛮=2 \ 𝛮\end{align}$$
(Μονάδες 5)4.4) Όταν η σφαίρα φτάνει στο έδαφος (11η λήψη) έχει κινηθεί για χρονικό διάστημα \(1 s\). Και έχει μετατοπιστεί κατά \(Δz\).
$$𝛥_𝑧=\frac{1}{2}\cdot 𝛼\cdot 𝑡^2_{11}=4 \ 𝑚$$
Συνεπώς η αρχική βαρυτική δυναμική ενέργεια της σφαίρας θα είναι:$$𝛦_{𝛥𝜐𝜈}= 𝑚\cdot 𝑔\cdot 𝛥_𝑧=40 \ 𝐽$$
Και η τελική κινητική
$$\begin{align}𝛫_{𝛵𝜀𝜆}− 𝛫_{𝛢𝜌𝜒}&=𝑊_{𝐹𝜊𝜆}\\ 𝛫_{𝛵𝜀𝜆}− 0&=𝑚\cdot 𝛼\cdot 𝛥_𝑧 \\ 𝛫_{𝛵𝜀𝜆}&=𝑚\cdot 𝛼\cdot 𝛥_𝑧=32 \ 𝐽\end{align}$$
(Μονάδες 8)
