Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 12280 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Άλγεβρα | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 14543 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 29-Απρ-2023 | Ύλη: | 2.1. Οι Πράξεις και οι Ιδιότητές τους 3.1. Εξισώσεις 1ου Βαθμού 3.3. Εξισώσεις 2ου Βαθμού | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Άλγεβρα | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 14543 | ||
| Ύλη: | 2.1. Οι Πράξεις και οι Ιδιότητές τους 3.1. Εξισώσεις 1ου Βαθμού 3.3. Εξισώσεις 2ου Βαθμού | ||
| Τελευταία Ενημέρωση: 29-Απρ-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Κάθε περιττός ακέραιος αριθμός α γράφεται στη μορφή \(a=2k+1\), \(k\) ακέραιος.
α) Να γράψετε τους αριθμούς \(3\), \(5\), \(7\) ως διαφορά τετραγώνων δύο ακεραίων.
(Μονάδες 6)
β)
i) Να αποδείξετε ότι η διαφορά των τετραγώνων δύο διαδοχικών ακεραίων ισούται πάντα με έναν περιττό ακέραιο.
(Μονάδες 6)
ii) Να γράψετε τον αριθμό \(2021\) ως διαφορά δύο τετραγώνων ακεραίων αριθμών.
(Μονάδες 6)
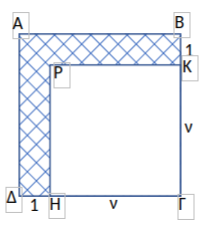
γ) Στο σχήμα τα τετράπλευρα \(ΑΒΓΔ\) και \(ΓΗΡΚ\) είναι τετράγωνα με \((ΓΗ)=(ΓΚ)=ν\) και \((ΒΚ)=(ΔΗ)=1\). Αν γνωρίζουμε ότι το γραμμοσκιασμένο εμβαδόν είναι ίσο με \(45\), να βρεθεί η τιμή του θετικού ακεραίου \(ν\).
(Μονάδες 7)
α) Έχουμε διαδοχικά:
$$3=4−1=2^{2}−1^{2}$$ $$5=3^{2}−2^{2}$$
και σκεπτόμενοι ότι:
$$7=Μ^{2}−Ν^{2}$$ $$=(Μ−Ν)(Μ+Ν)$$
ένα γινόμενο ακεραίων που δίνει \(7\) είναι οι \(1\), \(7\).
Αν \(Μ>Ν\) τότε \(Μ-Ν=1\), \(Μ+Ν=7\) και λύνοντας το σύστημα έχουμε με αντικατάσταση:
$$Μ=Ν+1$$
και
$$Ν+1 +Ν = 7$$
άρα \(2Ν = 6\), δηλαδή \(Ν = 3\) και \(Μ= 4\).
Οπότε:
$$7=4^{2}−3^{2}$$
β)
i) Έστω οι διαδοχικοί ακέραιοι \(k\), \(k+1\) , \(k\in ℤ\).
Η διαφορά των τετραγώνων τους είναι:
$$(k+1)^{2}−k^{2}=k^{2}+2k+1−k^{2}$$ $$=2k+1\ \text{,}\ k\in ℤ$$
Ο οποίος είναι περιττός αριθμός.
ii) Έχουμε ότι:
$$2021=2\cdot 1010+1$$
Από την απόδειξη στο προηγούμενο ερώτημα έχουμε:
$$2021=(1010+1)^{2}−(1010)^{2}$$ $$=1011^{2}−1010^{2}$$
γ) Η γραμμοσκιασμένη περιοχή έχει εμβαδόν όσο η διαφορά των εμβαδών των τετραγώνων \(ΑΒΓΔ\) και \(ΓΗΡΚ\).
Το τετράγωνο \(ΑΒΓΔ\) έχει πλευρά \(ν+1\), ενώ το \(ΓΗΡΚ\) έχει πλευρά \(ν\).
Ισχύει:
$$(ν+1)^{2}−ν^{2}=45$$
οπότε:
$$2ν+1=45 $$ $$\Leftrightarrow 2ν=44 $$ $$\Leftrightarrow ν=22$$