Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 19930 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Άλγεβρα | Τάξη: | Β' Λυκείου | |
| Κωδικός Θέματος: | 15060 | Θέμα: | 2 | |
| Τελευταία Ενημέρωση: | 10-Οκτ-2024 | Ύλη: | 3.2 Βασικές Τριγωνομετρικές Ταυτότητες | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Β' Λυκείου | ||
| Μάθημα: | Άλγεβρα | ||
| Θέμα: | 2 | ||
| Κωδικός Θέματος: | 15060 | ||
| Ύλη: | 3.2 Βασικές Τριγωνομετρικές Ταυτότητες | ||
| Τελευταία Ενημέρωση: 10-Οκτ-2024 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 2
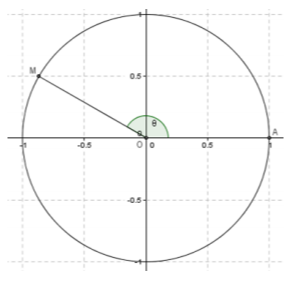
Στον τριγωνομετρικό κύκλο του σχήματος θεωρούμε το σημείο \(M\Big(x,\dfrac{1}{2}\Big)\) και τη γωνία \(θ\) με \(\dfrac{π}{2}<θ<π\) η οποία έχει αρχική πλευρά την \(ΟΑ\) και τελική την \(ΟΜ\).
α) Να αιτιολογήσετε γιατί ισχύει \(ημθ=\dfrac{1}{2}\).
(Μονάδες 5)
β) Να βρείτε το συνημίτονο της γωνίας \(θ\).
(Μονάδες 9)
γ) Να βρείτε τη γωνία \(θ\).
(Μονάδες 11)
ΛΥΣΗ
α) Η τεταγμένη του σημείου \(Μ\) είναι ίση με \(\dfrac{1}{2}\), οπότε \(ημθ=\dfrac{1}{2}\).
β) Η γωνία \(θ\) περιέχεται στο δεύτερο τεταρτημόριο, όπου ισχύει \(συνθ<0\). Από τη βασική ταυτότητα \(ημ^{2}θ+συν^{2}θ=1\), έχουμε:
$$συν^{2}θ=1-ημ^{2}θ=1-\dfrac{1}{4}=\dfrac{3}{4}$$
και επειδή ισχύει \(συνθ<0\), παίρνουμε \(συνθ=-\dfrac{\sqrt{3}}{2}\).
γ) Ισχύει \(ημθ=\dfrac{1}{2}=ημ\dfrac{π}{6}\) και \(\dfrac{π}{2}<θ<π\), οπότε η γωνία \(θ\) είναι η παραπληρωματική της γωνίας \(\dfrac{π}{6}\), δηλαδή \(θ=π-\dfrac{π}{6}=\dfrac{5π}{6}\).
