Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 39527 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Άλγεβρα | Τάξη: | Β' Λυκείου | |
| Κωδικός Θέματος: | 15422 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 10-Ιουν-2023 | Ύλη: | 3.1 Τριγωνομετρικοί Αριθμοί Γωνίας 3.2 Βασικές Τριγωνομετρικές Ταυτότητες 3.3 Αναγωγή στο 1o Τεταρτημόριο 3.4 Οι τριγωνομετρικές συναρτήσεις | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Β' Λυκείου | ||
| Μάθημα: | Άλγεβρα | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 15422 | ||
| Ύλη: | 3.1 Τριγωνομετρικοί Αριθμοί Γωνίας 3.2 Βασικές Τριγωνομετρικές Ταυτότητες 3.3 Αναγωγή στο 1o Τεταρτημόριο 3.4 Οι τριγωνομετρικές συναρτήσεις | ||
| Τελευταία Ενημέρωση: 10-Ιουν-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Δίνεται η συνάρτηση \(f(x)=aσυν(\dfrac{π}{2}-2x)-2ημ(π+2x)\) με \(a>0\), η οποία έχει μέγιστη τιμή το \(4\).
α) Να δείξετε ότι \(f(x)=(a+2)ημ2x\).
(Μονάδες 5)
β)
Να δείξετε ότι \(a=2\).
(Μονάδες 5)Να βρείτε την περίοδο της \(f\).
(Μονάδες 5)
γ) Να παραστήσετε γραφικά τη συνάρτηση \(f\) σε διάστημα μιας περιόδου.
(Μονάδες 5)
δ) Αν \(g(x)=5-συν^{2}2x\), να βρείτε, αν υπάρχουν, τα κοινά σημεία της \(C_{f}\) με την \(C_{g}\), όπου \(C_{f},C_{g}\) οι γραφικές παραστάσεις των \(f\), \(g\) αντίστοιχα.
(Μονάδες 5)
ΛΥΣΗ
α) Είναι:
$$f(x)=aσυν(\dfrac{π}{2}-2x)-2ημ(π+2x)$$ $$=aημ2x+2ημ2x$$ $$=(a+2)ημ2x$$
β)
- Η μέγιστη τιμή της συνάρτησης \(f\) καθορίζεται από το συντελεστή \(a+2\). Πρέπει δηλαδή:
$$a+2=4 $$ $$\Leftrightarrow α=2$$
- Η περίοδος \(Τ=\dfrac{2π}{2}=π\).
γ) Η γραφική παράσταση της \(f(x)=4ημ2x\) στο διάστημα \([0,π]\), βάσει του παρακάτω πίνακα:
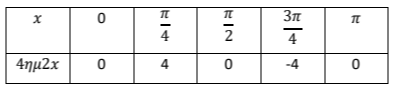
δίνεται στο παρακάτω σχήμα:
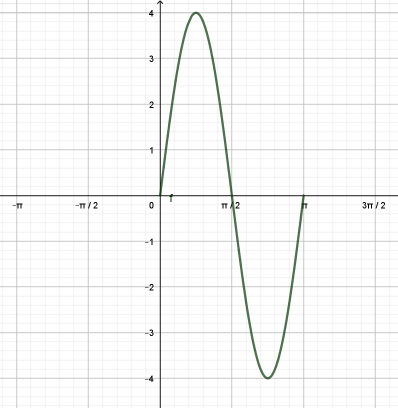
δ) Για να βρούμε τις τετμημένες των κοινών σημείων των δύο γραφικών παραστάσεων λύνουμε την εξίσωση:
$$f(x)=g(x) $$ $$\Leftrightarrow 4ημ2x=5-συν^{2}2x $$ $$\Leftrightarrow 4ημ2x=5-(1-ημ^{2}2x) $$ $$\Leftrightarrow ημ^{2}2x-4ημ2x+4=0 $$ $$\Leftrightarrow (ημ2x-2)^{2}=0 $$ $$\Leftrightarrow ημ2x=2\ \ \text{αδύνατη}$$
Αφού η παραπάνω εξίσωση είναι αδύνατη, δεν υπάρχουν σημεία τομής των δύο γραφικών παραστάσεων.