Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 20849 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Μαθηματικά Προσανατολισμού | Τάξη: | Γ' Λυκείου | |
| Κωδικός Θέματος: | 23196 | Θέμα: | 2 | |
| Τελευταία Ενημέρωση: | 04-Μαρ-2023 | Ύλη: | 1.3 Μονότονες συναρτήσεις - Αντίστροφη συνάρτηση 1.7 Όρια συνάρτησης στο άπειρο | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Γ' Λυκείου | ||
| Μάθημα: | Μαθηματικά Προσανατολισμού | ||
| Θέμα: | 2 | ||
| Κωδικός Θέματος: | 23196 | ||
| Ύλη: | 1.3 Μονότονες συναρτήσεις - Αντίστροφη συνάρτηση 1.7 Όρια συνάρτησης στο άπειρο | ||
| Τελευταία Ενημέρωση: 04-Μαρ-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 2
Δίνεται η συνάρτηση \(f(x)=e^{x}-1,x∈\mathbb{R}\).
α) Να αποδείξετε ότι αντιστρέφεται.
(Μονάδες 7)
β) Να βρείτε την \(f^{-1}\).
(Μονάδες 9)
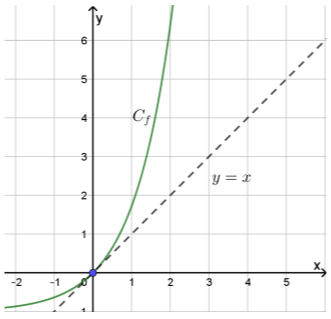
γ) Στο παρακάτω σχήμα δίνεται η γραφική παράσταση της συνάρτησης \(f\) και της ευθείας \(y=x\), η οποία εφάπτεται της \(C_f\) στο μοναδικό κοινό τους σημείο, την αρχή των αξόνων. Να σχεδιάσετε τη γραφική παράσταση της συνάρτησης \(f^{-1}\).
(Μονάδες 9)
α) Για κάθε \(x_{1},x_{2}∈\mathbb{R}\) με \(x_{1}\lt x_{2}\) έχουμε:
$$\begin{align} e^{x_{1}} & \lt e^{x_{2}}\\ \Leftarrow e^{x_{1}}-1&\lt e^{x_{2}}-1\\ \Leftarrow f(x_{1})&\lt f(x_{2})\end{align}$$
Άρα, η \(f\) είναι γνησίως αύξουσα στο \(\mathbb{R}\), οπότε είναι \(1-1\), άρα αντιστρέφεται.
β) Αν \(f(x)=y\), τότε έχουμε:
$$\begin{align} & f(x)=y \\ \Leftrightarrow & e^{x}-1=y\\ \Leftrightarrow & e^{x}=y+1\\ \Leftrightarrow & \begin{cases} x=\ln(y+1)\\ y+1>0 \end{cases}\\ \Leftrightarrow & \begin{cases} x=\ln(y+1)\\ y>-1 \end{cases}\end{align}$$
Άρα \(f^{-1}(x)=\ln(x+1),\ x>-1\).
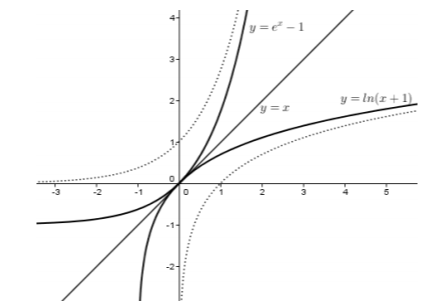
γ) Οι γραφικές παραστάσεις των συναρτήσεων \(f,f^{-1}\) είναι συμμετρικές ως προς την \(y=x\), οπότε η γραφική παράσταση της \(f^{-1}\) προκύπτει αφού φέρουμε την διχοτόμο \(y=x\) και θεωρήσουμε τη συμμετρική της \(C_{f}\), όπως φαίνεται στο σχήμα που ακολουθεί.
Σχόλιο
Στο σχήμα φαίνεται και μια εναλλακτική προσέγγιση του ερωτήματος, αφού η γραφική παράσταση της \(f^{-1}\), με βάση τον τύπο της, μπορεί να προκύψει από μετατόπιση της \(y=\ln x\) κατά μια μονάδα προς τα αριστερά.
Σε κάθε περίπτωση, αποδεικνύεται ότι οι γραφικές παραστάσεις των \(f,f^{-1}\) έχουν κοινή εφαπτομένη την διχοτόμο \(y=x\).
