Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 5584 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Μαθηματικά Προσανατολισμού | Τάξη: | Γ' Λυκείου | |
| Κωδικός Θέματος: | 26712 | Θέμα: | 2 | |
| Τελευταία Ενημέρωση: | 02-Μαρ-2023 | Ύλη: | 2.1 Η έννοια της παραγώγου | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Γ' Λυκείου | ||
| Μάθημα: | Μαθηματικά Προσανατολισμού | ||
| Θέμα: | 2 | ||
| Κωδικός Θέματος: | 26712 | ||
| Ύλη: | 2.1 Η έννοια της παραγώγου | ||
| Τελευταία Ενημέρωση: 02-Μαρ-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 2
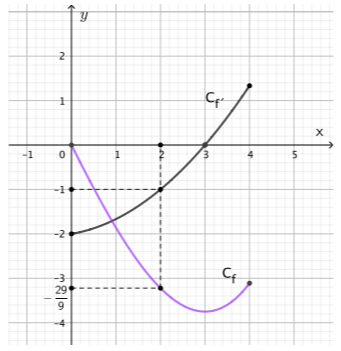
Στο παρακάτω σχήμα δίνονται οι γραφικές παραστάσεις μιας πολυωνυμικής συνάρτησης \(f\) τρίτου βαθμού ,η οποία είναι ορισμένη στο κλειστό διάστημα \([0,4]\), και της παραγώγου της, \(f'\).
α) Να βρείτε την κλίση της συνάρτησης \(f\) στο \(x_{ο}=2\).
(Μονάδες 06)
β) Να βρείτε την εξίσωση της εφαπτομένης (\(ε\)) της γραφικής παράστασης της \(f\) στο \(x_{ο}=2\).
(Μονάδες 10)
γ) Να υπολογίσετε τη γωνία που σχηματίζει η ευθεία (\(ε\)) με τον άξονα \(x'x\).
(Μονάδες 09)
ΛΥΣΗ
α) H κλίση της συνάρτησης \(f\) στο \(x_{o}=2\) ισούται με \(f'(2)\) Από τη γραφική παράσταση της συνάρτησης \(f'\) παρατηρούμε ότι \(f'(2)=-1\).
β) Η εξίσωση της εφαπτομένης (\(ε\)) της γραφικής παράστασης της \(f\) στο \(x_{ο}=2\) είναι:
$$y-f(2)=f'(2)(x-2)\ \ \ \ (1)$$
Από τη γραφική παράσταση της συνάρτησης \(f\) βρίσκουμε ότι:
$$f(2)=-\dfrac{29}{9}$$
Επομένως, η εξίσωση \((1)\) γίνεται:
$$y+\dfrac{29}{9}=-(x-2) $$ $$\Leftrightarrow y=-x+2-\dfrac{29}{9} $$ $$\Leftrightarrow y=-x-\dfrac{11}{9}$$
γ) Αν \(ω\) είναι η γωνία που σχηματίζει η ευθεία (\(ε\)) με τον άξονα \(x'x\), τότε:
$$εφω=f'(2)$$ $$=-1$$ $$=-εφ45^{ο}$$ $$=εφ(180^{ο}-45^{ο})$$ $$=εφ135^{ο}$$
Άρα, \(ω=135^{ο}\).