Θέμα: 26929

Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!

Τύπος Σχολείου:	Γενικό Λύκειο	Πηγή: Ι.Ε.Π.	Αναγνώσθηκε: 9038 φορές Επικοινωνία
Μάθημα:	Φυσική Προσανατολισμού	Τάξη:	Γ' Λυκείου
Κωδικός Θέματος:	26929	Θέμα:	2
Τελευταία Ενημέρωση:	29-Απρ-2023	Ύλη:	5.2 Κρούσεις 5.3 Κεντρική ελαστική κρούση δύο σφαιρών 2.3 Επαλληλία η Υπέρθεση κυμάτων 2.4 Συμβολή δύο κυμάτων στην επιφάνεια υγρού
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida)

Τύπος Σχολείου:	Γενικό Λύκειο
Τάξη:	Γ' Λυκείου
Μάθημα:	Φυσική Προσανατολισμού
Θέμα:	2
Κωδικός Θέματος:	26929
Ύλη:	5.2 Κρούσεις 5.3 Κεντρική ελαστική κρούση δύο σφαιρών 2.3 Επαλληλία η Υπέρθεση κυμάτων 2.4 Συμβολή δύο κυμάτων στην επιφάνεια υγρού
Τελευταία Ενημέρωση: 29-Απρ-2023
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida)

Αρχείο Εκφώνησης (PDF) Αρχείο Εκφώνησης (DOC)

ΘΕΜΑ 2
2.1. Στην επιφάνεια νερού υπάρχουν δύο σύμφωνες πηγές $1$ και $2$ οι οποίες δημιουργούν επιφανειακά κύματα. Στο σχήμα που ακολουθεί κάθε κύκλος αποτελείται από όλα τα σημεία του επίπεδου ελαστικού μέσου, στα οποία η κυματική διαταραχή από την πηγή που βρίσκεται στο κέντρο του φτάνει την ίδια στιγμή (μέτωπα των κυμάτων). Το σημείο $Α$ βρίσκεται στο μέσο της απόστασης ανάμεσα σε δύο διαδοχικούς κύκλους με κέντρο την πηγή $1$ (όπως φαίνεται στο σχήμα).

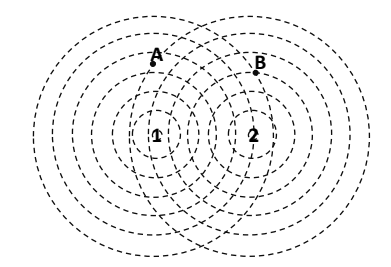
Στα σημεία $Α$ και $Β$ , το πλάτος του κύματος που είναι αποτέλεσμα της συμβολής θα είναι αντίστοιχα
(α) μέγιστο και ελάχιστο,
(β) μέγιστο και μέγιστο,
(γ) ελάχιστο και μέγιστο

2.1.Α. Να επιλέξετε την ορθή απάντηση.
Μονάδες 4

2.1.Β. Να αιτιολογήσετε την επιλογή σας.
Μονάδες 8

2.2. Εργαστηριακό αμαξίδιο $(1)$ κινείται προς δεύτερο εργαστηριακό αμαξίδιο $(2)$ και συγκρούεται με αυτό. Τα αμαξίδια βρίσκονται σε αεροτράπεζα και κινούνται σε ευθύγραμμη τροχιά στα άκρα της οποίας έχουν τοποθετηθεί αισθητήρες κίνησης, συνδεδεμένοι σε υπολογιστή, ώστε να υπολογίζεται η θέση κάθε αμαξιδίου σε συνάρτηση με τον χρόνο.

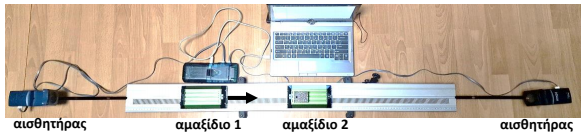
Με τη βοήθεια των μετρήσεων από τους αισθητήρες, σχεδιάστηκε το παρακάτω διάγραμμα.

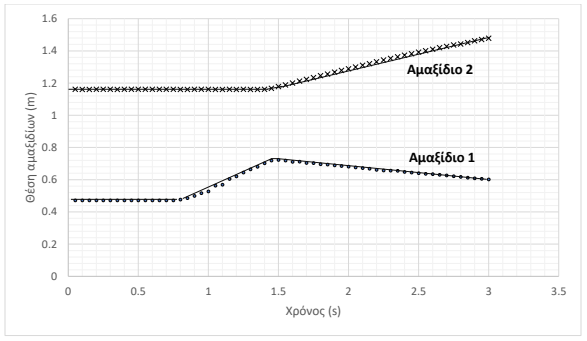
Το πηλίκο $m_{1} / m_{2}$ των μαζών των δύο αμαξιδίων είναι πιο κοντά στην τιμή
(α) $1$ ,
(β) $0, 5$
(γ) $0, 2$

2.2.Α. Να επιλέξετε την ορθή απάντηση.
Μονάδες 4

2.2.Β. Να αιτιολογήσετε την επιλογή σας.
Μονάδες 9

Εμφάνιση Απάντησης

Αρχείο Απάντησης (PDF) Αρχείο Απάντησης (DOC)

ΘΕΜΑ 2

2.1.
2.1.Α. Σωστή απάντηση η (γ)
Μονάδες 4

2.1.B.
Εξ ορισμού, η απόσταση ανάμεσα σε δύο μέτωπα κύματος (κύκλοι στο σχήμα) είναι ίση με ένα μήκος κύματος. Το σημείο $Α$ απέχει από τις πηγές $1$ και $2$ αντίστοιχα αποστάσεις $3, 5 λ$ και $6$ αντίστοιχα. (2 μονάδες)

Αυτό σημαίνει πως η διαφορά των αποστάσεων είναι $6 λ - 3, 5 λ = 2, 5 λ$ άρα τα κύματα από τις $2$ πηγές θα φτάσουν στο σημείο $Α$ με διαφορά φάσης $π$ . Αυτό σημαίνει ότι στο σημείο $Α$ θα υπάρχει αποσβετική συμβολή, δηλαδή ελάχιστο πλάτος. (2 μονάδες)

Το σημείο $Β$ απέχει από τις πηγές $1$ και $2$ αντίστοιχα αποστάσεις $6 λ$ και $3 λ$ αντίστοιχα. (2 μονάδες)

Αυτό σημαίνει πως η διαφορά των αποστάσεων είναι $6 λ - 3 λ = 3 λ$ άρα τα κύματα από τις $2$ πηγές θα φτάσουν στο σημείο $Β$ με διαφορά φάσης $0$ . Αυτό σημαίνει ότι στο σημείο $Β$ θα υπάρχει ενισχυτική συμβολή, δηλαδή μέγιστο πλάτος. (2 μονάδες)

Μονάδες 8

2.2.
2.2.Α. Σωστή απάντηση η (β)
Μονάδες 4

2.2.B.
Η ταχύτητα είναι ίση με την κλίση στο διάγραμμα θέσης-χρόνου. (1 μονάδα)

Οι ταχύτητες του αμαξιδίου 1 πριν και μετά την κρούση είναι αντίστοιχα: (2 μονάδες)

$v_{1} = \frac{Δ x}{Δ t} ≅ \frac{0, 72 - 0, 48}{1, 45 - 0, 80} m / s = 0, 32 m / s$

και

$v_{1}^{'} = \frac{Δ x}{Δ t} ≅ \frac{0, 60 - 0, 72}{3, 00 - 1, 45} m / s = - 0, 077 m / s$

Οι ταχύτητες του αμαξιδίου $2$ πριν και μετά την κρούση είναι αντίστοιχα: (2 μονάδες)

$v_{2} = \frac{Δ x}{Δ t} = 0 m / s$

και

$v_{2}^{'} = \frac{Δ x}{Δ t} = \frac{1, 48 - 1, 16}{3, 00 - 1, 45} m / s = 0, 21 m / s$

Εφαρμόζοντας την αρχή διατήρησης ορμής κατά την κρούση (θεωρώντας μονωμένο το σύστημα των δύο αμαξιδίων): (4 μονάδες)

$m_{1} v_{1} + m_{2} v_{2} = m_{1} v_{1}^{'} + m_{2} v_{2}^{'}$ $\Rightarrow m_{1} v_{1} - m_{1} v_{1}^{'} = m_{2} v_{2}^{'} - m_{2} v_{2}$ $\Rightarrow m_{1} (v_{1} - v_{1}^{'}) = m_{2} (v_{2}^{'} - v_{2})$ $\Rightarrow \frac{m_{1}}{m_{2}} = \frac{v_{2}^{'} - v_{2}}{v_{1} - v_{1}^{'}}$ $\Rightarrow \frac{m_{1}}{m_{2}} = \frac{0, 21 - 0}{0, 32 + 0, 08}$ $\Rightarrow \frac{m_{1}}{m_{2}} ≅ 0, 5$

Μονάδες 9