Θέμα: 31569

Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!

Τύπος Σχολείου:	Γενικό Λύκειο	Πηγή: Ι.Ε.Π.	Αναγνώσθηκε: 7066 φορές Επικοινωνία
Μάθημα:	Άλγεβρα	Τάξη:	Β' Λυκείου
Κωδικός Θέματος:	31569	Θέμα:	2
Τελευταία Ενημέρωση:	24-Φεβ-2023	Ύλη:	3.4 Οι τριγωνομετρικές συναρτήσεις
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida)

Τύπος Σχολείου:	Γενικό Λύκειο
Τάξη:	Β' Λυκείου
Μάθημα:	Άλγεβρα
Θέμα:	2
Κωδικός Θέματος:	31569
Ύλη:	3.4 Οι τριγωνομετρικές συναρτήσεις
Τελευταία Ενημέρωση: 24-Φεβ-2023
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida)

Αρχείο Εκφώνησης (PDF) Αρχείο Εκφώνησης (DOC)

ΘΕΜΑ 2

Δίνεται η συνάρτηση \(f(x)=-3συν2x\), \(x∈\mathbb{R}\)

α) Να βρείτε την περίοδο, τη μέγιστη και την ελάχιστη τιμή τηςσυνάρτησης \(f\).
(Μονάδες 12)

β) Να συμπληρώσετε τον παρακάτω πίνακα τιμών και να παραστήσετε γραφικά τη συνάρτηση \(f\) σε διάστημαμιας περιόδου.
(Μονάδες 13)

\(x\)	\(0\)	\(\dfrac{π}{4}\)	\(\dfrac{π}{2}\)	\(\dfrac{3π}{4}\)	\(π\)
\(2x\)
\(συν2x\)
\(f(x)=-3συν2x\)

Εμφάνιση Απάντησης

Αρχείο Απάντησης (PDF) Αρχείο Απάντησης (DOC)

ΛΥΣΗ

α) Η συνάρτηση \(f(x)=-3συν2x\) είναι της μορφής \(f(x)=ρσυν(ωx)\), με \(ρ=-3\) και \(ω=2\). Άρα η περίοδος της \(f\) είναι \(Τ=\dfrac{2π}{ω}=\dfrac{2π}{2}=π\), η μέγιστη τιμή της είναι \(3\) και η ελάχιστη είναι \(-3\).

β) Σε διάστημα πλάτους μιας περιόδου, δηλαδή \(π\), έχουμε τον παρακάτω πίνακα τιμών της συνάρτησης \(f\) :

\(x\)	\(0\)	\(\dfrac{π}{4}\)	\(\dfrac{π}{2}\)	\(\dfrac{3π}{4}\)	\(π\)
\(2x\)	\(0\)	\(\dfrac{π}{2}\)	\(π\)	\(\dfrac{3π}{2}\)	\(2π\)
\(συν2x\)	\(1\)	\(0\)	\(-1\)	\(0\)	\(1\)
\(f(x)=-3συν2x\)	\(-3\)	\(0\)	\(3\)	\(0\)	\(-3\)

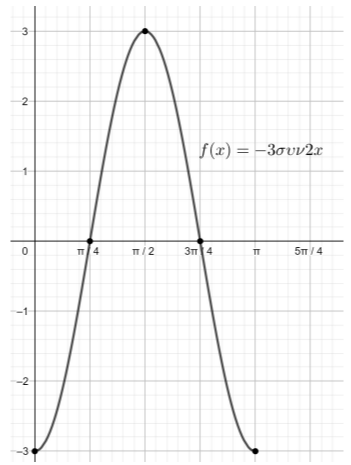
Επομένως η γραφική παράσταση της συνάρτησης \(f\) στο διάστημα \([0,π]\) δίνεται από το παρακάτω σχήμα: