Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 10674 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική Προσανατολισμού | Τάξη: | Γ' Λυκείου | |
| Κωδικός Θέματος: | 34115 | Θέμα: | 2 | |
| Τελευταία Ενημέρωση: | 21-Μαΐ-2023 | Ύλη: | 2.4 Συμβολή δύο κυμάτων στην επιφάνεια υγρού 7.4 Φαινόμενο Compton | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Γ' Λυκείου | ||
| Μάθημα: | Φυσική Προσανατολισμού | ||
| Θέμα: | 2 | ||
| Κωδικός Θέματος: | 34115 | ||
| Ύλη: | 2.4 Συμβολή δύο κυμάτων στην επιφάνεια υγρού 7.4 Φαινόμενο Compton | ||
| Τελευταία Ενημέρωση: 21-Μαΐ-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 2
2.1. Στην επιφάνεια υγρού που ηρεμεί,σε ορισμένο σημείο \(Π\), δημιουργούμε με τη βοήθεια σημειακής πηγής, αρμονικά εγκάρσια κύματα συχνότητας \(f\). Τα κύματα αυτά, φτάνουν σε ακίνητο ανιχνευτή \(Α\) απευθείας, με διάδοση στη διεύθυνση \(ΠΑ\), αλλά και μετά από ανάκλαση σε ανακλαστήρα \(α\). Ο ανακλαστήρας, είναι μια μικρή μεταλλική επιφάνεια, που μπορούμε να την μετακινούμε πάνω στη μεσοκάθετο του ευθύγραμμου τμήματος \(ΠΑ\). Για τις διαστάσεις του πειράματος, μπορούμε να θεωρήσουμε ότι, τα κύματα που φτάνουν στον ανιχνευτή \(Α\), έχουν ίσα πλάτη. Η απόσταση του σημείου \(Π\) από τον ανιχνευτή \(Α\) είναι \(d=6\cdot λ\), όπου \(λ\) το μήκος κύματος των κυμάτων που παράγει η πηγή, στην επιφάνεια του υγρού.
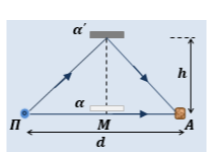
Αρχίζουμε να μετακινούμε αργά τον ανακλαστήρα πάνω στη μεσοκάθετο του \(ΠΑ\), ξεκινώντας από μια θέση \(α\) πολύ κοντά στο μέσο \(Μ\) του \(ΠΑ\), όπως στο σχήμα. Κατά τη μετακίνηση αυτή, παρατηρούμε στον ανιχνευτή \(Α\), ταλαντώσεις με πλάτος που μεταβάλλεται.
Το πλάτος ταλαντώσεων στον ανιχνευτή, μεγιστοποιείται για τέταρτη φορά μετά την έναρξη της μετακίνησης του ανακλαστήρα, όταν τον έχουμε μετατοπίσει πάνω στη μεσοκάθετο κατά \(h\).
Η ταχύτητα διάδοσης των κυμάτων στην επιφάνεια του υγρού είναι:
α. \(υ_{δ}=\dfrac{h\cdot f}{4}\),
β. \(υ_{δ}=h\cdot f\),
γ. \(υ_{δ}=4\cdot h\cdot f\)
2.1.Α. Να επιλέξετε τη σωστή απάντηση.
Μονάδες 4
2.1.Β. Να αιτιολογήσετε την επιλογή σας.
Μονάδες 8
2.2. Μελετώντας την πρόσπτωση ακτινών \(X\), σε μια επιφάνεια, ο Compton περιέγραψε την σκέδαση των φωτονίων μήκους κύματος \(λ\) μέσω της σχέσης ( \(λ'-λ=\dfrac{h}{m\cdot c}(1-συνφ)\) ), όπου \(h\) είναι η σταθερά Planck, \(m\) η μάζα του ηλεκτρονίου και \(c\) η ταχύτητα του φωτός. Η ποσότητα \(\dfrac{h}{m\cdot c}\), έχει διαστάσεις μήκους κύματος και ονομάζεται μήκος κύματος Compton των ηλεκτρονίων ( \(λ_{c}=\dfrac{h}{m\cdot c}\) ).
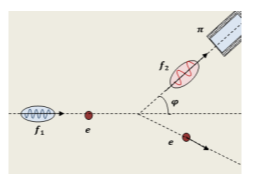
Μια δέσμη φωτονίων με μήκος κύματος ίσο με το μισό του μήκους κύματος Compton ( \(λ=\dfrac{λ_{c}}{2}\) ) σκεδάζεται από τα ηλεκτρόνια ενός στόχου από άνθρακα. Αν ανιχνεύσαμε σκεδαζόμενη δέσμη φωτονίων με κατάλληλο “παράθυρο”, και γωνία σκέδασης \(φ=60^{0}\), όπως στο σχήμα, το ποσοστό της αρχικής ενέργειας ενός φωτονίου που μετατρέπεται σε κινητική ενέργεια του σκεδαζόμενου ηλεκτρονίου στη σκέδαση αυτή είναι:
(α) \(100\%\),
(β) 50%,
(γ) 20%
2.2.Α. Να επιλέξετε τη σωστή απάντηση.
Μονάδες 4
2.2.Β. Να αιτιολογήσετε την επιλογή σας.
Μονάδες 9
ΘΕΜΑ 2
2.1.
2.1.Α. Σωστή απάντηση η (α)
Μονάδες 4
2.1.B. Καθώς μετακινούμε τον ανακλαστήρα \(α\), πάνω στην μεσοκάθετο του ευθύγραμμου τμήματος \(ΠΑ\), στον ανιχνευτή \(Α\) φτάνουν δύο κύματα, τα οποία ξεκινούν από την πηγή \(Π\) και διατρέχουν διαφορετικές αποστάσεις μέχρι να φτάσουν σε αυτόν.
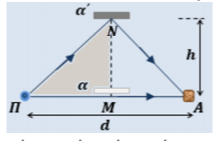
Ανιχνεύουμε ταλάντωση μέγιστου πλάτους στον ανιχνευτή, για τέταρτη φορά από τότε που αρχίσαμε να μετακινούμε τον ανακλαστήρα α, όταν για τις αποστάσεις αυτές, ισχύει η σχέση:
$$r_{1}-r_{2}=4\cdot λ$$ $$\Rightarrow (ΠΝ)+(ΝΑ)-(ΠΑ)=4\cdot λ$$ $$\Rightarrow 2\cdot (ΠΝ)-(ΠΑ)=4\cdot λ$$ $$\Rightarrow 2\cdot (ΠΝ)=d+4\cdot λ$$ $$=6\cdot λ+4\cdot λ$$ $$=10\cdot λ$$ $$\Rightarrow (ΠΝ)=5\cdot λ$$
Εφαρμόζουμε πυθαγόρειο θεώρημα στο ορθογώνιο τρίγωνο \(ΠΜΝ\) :
$$(ΠΝ)^{2}=(ΠΜ)^{2}+(ΜΝ)^{2}$$ $$\Rightarrow (5\cdot λ)^{2}=(\dfrac{d}{2})^{2}+h^{2}$$ $$\Rightarrow h^{2}=(5\cdot λ)^{2}-(3\cdot λ)^{2}=16\cdot λ^{2}$$ $$\Rightarrow h=4\cdot λ=4\cdot \dfrac{υ_{δ}}{f}$$ $$\Rightarrow υ_{δ}=\dfrac{h\cdot f}{4}$$
Μονάδες 8
2.2.
2.2.Α. Σωστή απάντηση η (β)
Μονάδες 4
2.2.B. Εφαρμόζουμε την εξίσωση Compton για να υπολογίσουμε το μήκος κύματος του σκεδαζόμενου φωτονίου σε σχέση με το μήκος κύματος Compton ( \(λ_{c})\), επειδή δίνεται για το μήκος κύματος του προσπίπτοντος φωτονίου, ότι ισχύει \(λ=\dfrac{λ_{c}}{2}\).
Άρα:
$$λ'-λ=\dfrac{h}{m\cdot c}(1-συν60^{0})$$ $$=λ_{c}(1-\dfrac{1}{2})$$ $$=\dfrac{λ_{c}}{2}$$ $$\Rightarrow λ'=λ+\dfrac{λ_{c}}{2}$$ $$=\dfrac{λ_{c}}{2}+\dfrac{λ_{c}}{2}=λ_{c}$$
Εφαρμόζοντας την διατήρηση της ενέργειας, η κινητική ενέργεια του ανακρουόμενου ηλεκτρονίου, είναι ίση με την απώλεια ενέργειας του φωτονίου κατά τη σκέδαση αυτή:
$$K_{e}=h\cdot f-h\cdot f'$$ $$=h\cdot (\dfrac{c}{λ}-\dfrac{c}{λ'})$$ $$=h\cdot c\cdot (\dfrac{2}{λ_{c}}-\dfrac{1}{λ_{c}})$$ $$=\dfrac{h\cdot c}{λ_{c}}$$
Το ποσοστό της ενέργειας του φωτονίου που μεταβιβάζεται στο ανακρουόμενο ηλεκτρόνιο είναι:
$$π=\dfrac{K_{e}}{h\cdot f}\cdot 100\%$$ $$=\dfrac{\dfrac{h\cdot c}{λ_{c}}}{\dfrac{2\cdot h\cdot c}{λ_{c}}}\cdot 100\%$$ $$=50\%$$
Μονάδες 9
