Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 9132 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική Προσανατολισμού | Τάξη: | Γ' Λυκείου | |
| Κωδικός Θέματος: | 34117 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 21-Μαΐ-2023 | Ύλη: | 1.3 Απλή αρμονική ταλάντωση 1.5 Φθίνουσες ταλαντώσεις 7.2 Η ακτινοβολία του μέλανος σώματος | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Γ' Λυκείου | ||
| Μάθημα: | Φυσική Προσανατολισμού | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 34117 | ||
| Ύλη: | 1.3 Απλή αρμονική ταλάντωση 1.5 Φθίνουσες ταλαντώσεις 7.2 Η ακτινοβολία του μέλανος σώματος | ||
| Τελευταία Ενημέρωση: 21-Μαΐ-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Μικρή σφαίρα μάζας \(m=200\ g\), κρέμεται στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς \(k=20\ \dfrac{N}{m}\), το πάνω άκρο του οποίου έχει στερεωθεί σε ακλόνητο σημείο-οροφή, όπως στο σχήμα και το σύστημα αρχικά ισορροπεί ακίνητο.
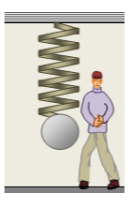
Εκτρέπουμε το σύστημα από την αρχική θέση ισορροπίας του, μετατοπίζοντας αργά τη σφαίρα, κατακόρυφα προς τα κάτω κατά \(20\ cm\) και από τη θέση αυτή την αφήνουμε ελεύθερη τη χρονική στιγμή \(t_{0}=0\) να εκτελεί ταλαντώσεις.
4.1. Αν υποθέσουμε ότι κατά την κίνηση της σφαίρας θα μπορούσαμε να αγνοήσουμε τις δυνάμεις αντίστασης του αέρα πάνω της, να αποδείξετε ότι θα εκτελούσε απλή αρμονική ταλάντωση και να υπολογίσετε την περίοδο και την ενέργεια ταλάντωσης.
Μονάδες 6
Ως πιο ρεαλιστική προσέγγιση, μελετάμε την κίνηση της σφαίρας συνυπολογίζοντας την αντίσταση του αέρα, που είναι της μορφής \(F_{\text{αντ}}=-b\cdot υ\), όπου \(b\) η σταθερά απόσβεσης και \(υ\) η στιγμιαία ταχύτητα της σφαίρας. Έτσι η σφαίρα εκτελεί φθίνουσα ταλάντωση με πλάτος που μειώνεται με το χρόνο σύμφωνα με τη σχέση \(A=A_{0}\cdot e^{-Λ\cdot t}\). Επειδή η σταθερά απόσβεσης \(b\) είναι αρκετά μικρή, μπορούμε να υποθέσουμε ότι η θέση ισορροπίας του συστήματος είναι σταθερή και συμπίπτει με την αρχική του θέση ισορροπίας, ότι η περίοδος της φθίνουσας είναι ίση με την περίοδο της αμείωτης ταλάντωσης που θα εκτελούσε το σύστημα, αν δεν υπήρχαν αντιστάσεις αέρα και ότι η ενέργεια ταλάντωσης μπορεί να υπολογίζεται από τη σχέση \(E_{\text{ταλ}}=\dfrac{1}{2}\cdot k\cdot A^{2}\), όπου \(A\) το πλάτος της. Δίνεται επίσης ότι για τη σταθερά \(Λ\) και τη σταθερά απόσβεσης \(b\), ισχύει η σχέση \(Λ=\dfrac{b}{2\cdot m}\). Μετρήσαμε ότι το πλάτος της φθίνουσας ταλάντωσης, έγινε ίσο με το μισό του αρχικού της πλάτους, τη χρονική στιγμή \(t=14\ s\).
4.2. Να υπολογίσετε τη σταθερά απόσβεσης \(b\).
Μονάδες 6
Αν υποθέσουμε ότι το σύστημα αυτό αποτελεί ένα κβαντικό ταλαντωτή (ταλαντωτή που η ενέργειά του μπορεί να πάρει μόνο διακριτές τιμές), να υπολογίσετε:
4.3. το κβάντο ενέργειας αυτού του ταλαντωτή (το ενεργειακό διάστημα, μεταξύ δύο διαδοχικών επιτρεπόμενων ενεργειακών σταθμών του).
Μονάδες 6
4.4. το πλήθος των ενεργειακών κβάντων που απέβαλε το σύστημα από την έναρξη των ταλαντώσεων, μέχρι τη στιγμή \(t=14\ s\). Με βάση τα αποτελέσματά σας, πιστεύετε ότι μπορούμε να εφαρμόσουμε την κβαντική θεωρία στο μακρόκοσμο;
Μονάδες 7
Να υποθέσετε κατά προσέγγιση ότι το μέτρο της επιτάχυνσης βαρύτητας είναι \(g\approxeq 10\ \dfrac{m}{s^{2}}\), ότι ισχύει \(ln2\approxeq 0,7\) και ότι η σταθερά του Planck είναι \(h\approxeq 2\cdot π\cdot 10^{-34}\ J\cdot s\).
ΘΕΜΑ 4
4.1. Καθώς το σύστημα αρχικά ισορροπεί (Θ.Ι), το ελατήριο έχει επιμηκυνθεί κατά \(Δl\) σε σχέση με το φυσικό του μήκος, η σφαίρα δέχεται το βάρος της και τη δύναμη του ελατηρίου και ισχύει:
$$(ΣF)_{\text{Θ.Ι}}=0 $$ $$\Rightarrow m\cdot g=k\cdot Δl\ \ \ \ (1)$$
Κατεβάζουμε αργά και κατακόρυφα προς τα κάτω τη σφαίρα κατά \(y_{0}=0,2\ m\) από τη θέση ισορροπίας της και από τη θέση αυτή την αφήνουμε ελεύθερη τη στιγμή \(t_{0}=0\).
Τη στιγμή ακριβώς που η σφαίρα αφήνεται ελεύθερη να κινηθεί ισχύει:
$$(ΣF)_{Δ}=m\cdot g-k\cdot (Δl+y_{0})\ \ \ \ (2)$$
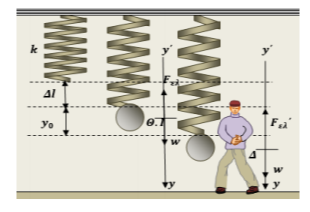
Συνδυάζοντας τις εξισώσεις \((1)\) και \((2)\), προκύπτει:
$$(ΣF)_{Δ}=-k\cdot y_{0}\ \ \ \ (3)$$
Αυτή όμως είναι η ικανή και αναγκαία συνθήκη της απλής αρμονικής ταλάντωσης. Άρα η σφαίρα εκτελεί απλή αρμονική ταλάντωση από τη στιγμή που την αφήσαμε ελεύθερη και εφόσον μπορούμε να αγνοήσουμε τις αντιστάσεις του αέρα πάνω της.
Η σταθερά επαναφοράς της απλής αρμονικής ταλάντωσης είναι η σταθερά του ελατηρίου, όπως προκύπτει από σχέση (3), οπότε η περίοδος της ταλάντωσης είναι:
$$T=2\cdot π\cdot \sqrt{\dfrac{m}{k}}$$ $$=2\cdot π\cdot \sqrt{\dfrac{0,2}{20}}\ s$$ $$=0,2\cdot πs$$
Επειδή τη χρονική στιγμή \(t_{0}=0\) αφήσαμε τη σφαίρα ελεύθερη να κινηθεί χωρίς αρχική ταχύτητα, η θέση αυτή αποτελεί ακραία θέση ταλάντωσης, οπότε το πλάτος \(A\) της ταλάντωσης είναι:
$$A=y_{0}=0,2\ m$$
Η ενέργεια ταλάντωσης είναι:
$$E_{\text{ταλ}}=\dfrac{1}{2}\cdot k\cdot A^{2}$$ $$=\dfrac{1}{2}\cdot 20\cdot 0,04\ J=0,4\ J$$
Μονάδες 6
4.2. Εφαρμόζουμε την εξίσωση της εκθετικής μείωσης του πλάτους για το χρονικό διάστημα από τη στιγμή \(t_{0}=0\) που αφήσαμε τη σφαίρα ελεύθερη να κινηθεί, μέχρι τη στιγμή \(t=14\ s\), κατά την οποία το πλάτος έγινε ίσο με το μισό του αρχικού:
$$\dfrac{A_{0}}{2}=A_{0}\cdot e^{-Λ\cdot t}$$ $$\Rightarrow e^{-Λ\cdot t}=\dfrac{1}{2}$$ $$\Rightarrow Λ=\dfrac{ln2}{t}\approxeq \dfrac{0,7}{14}\ s^{-1}=0,05\ s^{-1}$$
Έτσι προκύπτει:
$$\dfrac{b}{2\cdot m}=0,05\ s^{-1}$$ $$ b=2\cdot 0,2\cdot 0,05\ kg\cdot s^{-1}=0,02\ kg\cdot s^{-1}$$
Μονάδες 6
4.3. Αν μπορούσαμε να θεωρήσουμε κβαντικό τον ταλαντωτή, τότε το κβάντο ενέργειας, δηλαδή η διαφορά ενέργειας δύο διαδοχικών επιτρεπόμενων καταστάσεων για αυτόν, θα ήταν:
$$E_{\text{κβ.}}=h\cdot f=\dfrac{h}{T}$$ $$=\dfrac{2\cdot π\cdot 10^{-34}\ J\cdot s}{0,2\cdot πs}=10^{-33}\ J$$
Μονάδες 6
4. 4. Στο χρονικό διάστημα από τη στιγμή \(t_{0}=0\) που αφήσαμε τη σφαίρα ελεύθερη να κινηθεί, μέχρι τη στιγμή \(t=14\ s\), κατά την οποία το πλάτος έγινε ίσο με το μισό του αρχικού, ο ταλαντωτής έχει χάσει ενέργεια:
$$ΔE=\dfrac{1}{2}\cdot k\cdot A_{0}^{2}-\dfrac{1}{2}\cdot k\cdot (\dfrac{A_{0}}{2})^{2}$$ $$=\dfrac{1}{2}\cdot k\cdot (A_{0}^{2}-\dfrac{A_{0}^{2}}{4})$$ $$=\dfrac{3\cdot k}{8}\cdot A_{0}^{2}$$ $$=\dfrac{3}{8}\cdot 20\cdot 0,04\ J=0,3\ J$$
Το πλήθος των κβάντων ενέργειας που θα είχαν αποβληθεί, για αυτή την απώλεια ενέργειας, αν θεωρούσαμε τον ταλαντωτή κβαντικό, προκύπτει:
$$ΔE=n\cdot E_{\text{κβ.}}$$ $$\Rightarrow n=\dfrac{ΔE}{E_{\text{κβ.}}}$$ $$=\dfrac{0,3}{10^{-33}}=3\cdot 10^{32}\ \text{κβάντα}$$
Προφανώς, πρόκειται για ένα τεράστιο πλήθος κβάντων, σε μια τόσο μικρή διαφορά ενέργειας. Αυτό σημαίνει ότι πρέπει να θεωρήσουμε συνεχή την απώλεια ενέργεια του συστήματος και όχι κβαντισμένη. Δεν μπορεί να εφαρμοστεί η κβαντική θεωρία στον μακρόκοσμο.
Μονάδες 7