Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 4873 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Γεωμετρία | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 34314 | Θέμα: | 2 | |
| Τελευταία Ενημέρωση: | 17-Απρ-2024 | Ύλη: | 3.1. Είδη και στοιχεία τριγώνων 4.6. Άθροισμα γωνιών τριγώνου 5.9. Μια ιδιότητα του ορθογώνιου τριγώνου | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Γεωμετρία | ||
| Θέμα: | 2 | ||
| Κωδικός Θέματος: | 34314 | ||
| Ύλη: | 3.1. Είδη και στοιχεία τριγώνων 4.6. Άθροισμα γωνιών τριγώνου 5.9. Μια ιδιότητα του ορθογώνιου τριγώνου | ||
| Τελευταία Ενημέρωση: 17-Απρ-2024 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 2
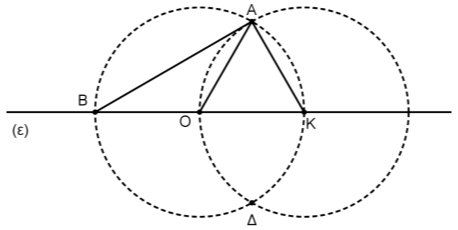
Θεωρούμε δυο ίσους κύκλους \((Ο,ρ)\) και \((Κ,ρ)\) τεμνόμενους στα σημεία \(Α\) και \(Δ\), με τα κέντρα τους \(Ο\) και \(Κ\) να βρίσκονται σε ευθεία \((ε)\) που τέμνει τον κύκλο \((Ο,ρ)\) σε σημείο \(Β\), και τη διάκεντρό τους \(ΟΚ\) να είναι ίση με \(ρ\).
α) Να αποδείξετε ότι:
το τρίγωνο \(ΟΑΚ\) είναι ισόπλευρο,
(Μονάδες 7)το τρίγωνο \(ΑΒΚ\) είναι ορθογώνιο.
(Μονάδες 9)
β) Να υπολογίσετε τη γωνία \(ΑΒΚ\).
(Μονάδες 9)
ΛΥΣΗ

α)
Από τα δεδομένα έχουμε ότι οι κύκλοι με κέντρα τα σημεία \(Ο\) και \(Κ\) είναι ίσοι ακτίνας \(ρ\). Οπότε θα είναι \(ΑΟ = ΟΚ = ρ\), ως ακτίνες του κύκλου με κέντρο το \(Ο\). Ισχύει επίσης ότι \(ΚΑ = ρ\) ως ακτίνα του κύκλου κέντρου \(Κ\). Άρα \(ΑΟ = ΟΚ = ΚΑ = ρ\ \ \ (1)\). Επομένως το τρίγωνο \(ΟΑΚ\) είναι ισόπλευρο.
Στο τρίγωνο \(ΑΒΚ\), η πλευρά του \(ΒΚ\) είναι διάμετρος του κύκλου \((Ο, ρ)\) και το \(Ο\) είναι το μέσο της ως κέντρο του κύκλου οπότε ισχύει ότι \(ΟΒ = ΟΚ = ρ\ \ \ (2)\) και άρα το τμήμα \(ΑΟ\) είναι διάμεσος στην πλευρά \(ΒΓ\). Από τις σχέσεις \((1)\) και \((2)\) έχουμε ότι \(ΑΟ = ΟΒ = ΟΚ\) ή \(ΑΟ = \dfrac{ΒΚ}{2}\). Επομένως η διάμεσος \(ΑΟ\) που αντιστοιχεί στην πλευρά \(ΒΚ\) του τριγώνου \(ΑΒΚ\) είναι ίση με το μισό της, άρα το τρίγωνο \(ΑΒΚ\) είναι ορθογώνιο με υποτείνουσα την πλευρά \(ΒΓ\).
β) Από το αi) ερώτημα έχουμε ότι το τρίγωνο \(ΟΑΚ\) είναι ισόπλευρο, οπότε \(\hat{ΒΚΑ} = 60^0\). Από το αii) ερώτημα έχουμε ότι το τρίγωνο \(ΑΒΚ\) είναι ορθογώνιο με υποτείνουσα την \(ΒΚ\), οπότε \(\hat{ΒΑΚ} = 90^0\). Για τις γωνίες του τριγώνου \(ΒΑΚ\) ισχύει ότι \(\hat{ΒΑΚ} + \hat{ΒΚΑ} + \hat{ΑΒΚ} = 180^0\), οπότε θα έχουμε \(90^0 + 60^0 + \hat{ΑΒΚ} = 180^0\) ή \(\hat{ΑΒΚ} = 30^0\).
