Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 14795 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Γεωμετρία | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 34387 | Θέμα: | 2 | |
| Τελευταία Ενημέρωση: | 20-Νοε-2023 | Ύλη: | 3.2. 1ο Κριτήριο ισότητας τριγώνων 3.3. 2ο Κριτήριο ισότητας τριγώνων 3.6. Κριτήρια ισότητας ορθογώνιων τριγώνων | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Γεωμετρία | ||
| Θέμα: | 2 | ||
| Κωδικός Θέματος: | 34387 | ||
| Ύλη: | 3.2. 1ο Κριτήριο ισότητας τριγώνων 3.3. 2ο Κριτήριο ισότητας τριγώνων 3.6. Κριτήρια ισότητας ορθογώνιων τριγώνων | ||
| Τελευταία Ενημέρωση: 20-Νοε-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 2
Δίνεται ισοσκελές τρίγωνο \(ΑΒΓ\) (\(ΑΒ = ΑΓ\)) και οι διχοτόμοι του \(ΒΔ\) και \(ΓΕ\) των γωνιών \(Β\) και \(Γ\) αντίστοιχα.
α) Να αποδείξετε ότι τα τρίγωνα \(ΒΓΔ\) και \(ΓΒΕ\) είναι ίσα.
(Μονάδες 13)
β) Έστω \(ΕΗ\) και \(ΔΖ\) οι κάθετες από τα σημεία \(Ε\) και \(Δ\) αντίστοιχα στη \(ΒΓ\). Να αποδείξετε ότι
\(ΕΗ = ΔΖ\).
(Μονάδες 12)
ΛΥΣΗ
Έστω ισοσκελές τρίγωνο \(ΑΒΓ\) με \(ΑΒ = ΑΓ\) και \(ΒΔ\), \(ΓΕ\) διχοτόμοι των γωνιών του \(Β\), \(Γ\) αντίστοιχα.
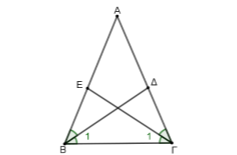
α) Τα τρίγωνα \(ΒΓΔ\) και \(ΓΒΕ\) έχουν:
- \(ΒΓ\) κοινή πλευρά
- \(\hat{Β} = \hat{Γ}\) γωνίες βάσης ισοσκελούς τριγώνου
- \(\hat{Β_1}=\dfrac{\hat{B}}{2}=\dfrac{\hat{Γ}}{2}=\hat{Γ_1}\) ως μισά των ίσων γωνιών \(Β\) και \(Γ\) του ισοσκελούς τριγώνου \(ΑΒΓ\).
Τα τρίγωνα \(ΒΓΔ\) και \(ΓΒΕ\) είναι ίσα γιατί έχουν μια πλευρά και τις προσκείμενες σε αυτή γωνίες ίσες μία προς μία (\(ΓΠΓ\)).
β) Έστω \(ΕΗ\) και \(ΔΖ\) οι κάθετες στην πλευρά \(ΒΓ\).
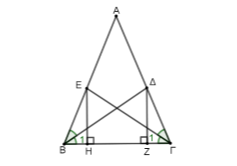
Από το α) ερώτημα τα τρίγωνα \(ΒΓΔ\) και \(ΓΒΕ\) είναι ίσα, άρα θα είναι ίσες και οι πλευρές τους \(ΒΕ\) και \(ΓΔ\) που βρίσκονται απέναντι από τις ίσες γωνίες \(\hat{Γ_1}\) και \(\hat{Β_1}\) αντίστοιχα. \((1)\)
Τα τρίγωνα \(ΕΒΗ\) και \(ΔΖΓ\) έχουν:
- \(\hat{Η}=\hat{Ζ}=90^0\) (αφού \(ΕΗ\) και \(ΔΖ\) είναι κάθετες στη \(ΒΓ\))
- \(\hat{Β} = \hat{Γ}\) (ως γωνίες προσκείμενες στη βάση του ισοσκελούς τριγώνου \(ΑΒΓ\))
- \(BE = ΓΔ\) από \((1)\)
Άρα είναι ίσα γιατί είναι ορθογώνια με ίσες υποτείνουσες και μία οξεία γωνία ίση αντίστοιχα ίσες μία προς μία. Οπότε είναι και \(EH = ΔZ\) ως πλευρές που βρίσκονται απέναντι από τις ίσες γωνίες \(\hat{Β}\) και \(\hat{Γ}\) αντίστοιχα.
