Θέμα: 34780

Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!

Τύπος Σχολείου:	Γενικό Λύκειο	Πηγή: Ι.Ε.Π.	Αναγνώσθηκε: 8102 φορές Επικοινωνία
Μάθημα:	Γεωμετρία	Τάξη:	Α' Λυκείου
Κωδικός Θέματος:	34780	Θέμα:	2
Τελευταία Ενημέρωση:	20-Νοε-2023	Ύλη:	3.2. 1ο Κριτήριο ισότητας τριγώνων 3.3. 2ο Κριτήριο ισότητας τριγώνων
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida)

Τύπος Σχολείου:	Γενικό Λύκειο
Τάξη:	Α' Λυκείου
Μάθημα:	Γεωμετρία
Θέμα:	2
Κωδικός Θέματος:	34780
Ύλη:	3.2. 1ο Κριτήριο ισότητας τριγώνων 3.3. 2ο Κριτήριο ισότητας τριγώνων
Τελευταία Ενημέρωση: 20-Νοε-2023
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida)

Αρχείο Εκφώνησης (PDF) Αρχείο Εκφώνησης (DOC)

ΘΕΜΑ 2

Στις προεκτάσεις των πλευρών $Β Α$ και $Γ Α$ (προς το $Α$ ) τριγώνου $Α Β Γ$ παίρνουμε τα τμήματα $Α Δ = Α Β$ και $Α Ε = Α Γ$ .

α) Να αποδείξετε ότι $Δ Ε = Β Γ$ .
(Μονάδες 12)

β) Αν $Α Μ$ είναι η διάμεσος του τριγώνου $Α Β Γ$ και η προέκταση της $Α Μ$ τέμνει την $Ε Δ$ στο $Ζ$ , να αποδείξετε ότι:

τα τρίγωνα $Α Δ Ζ$ και $Α Β Μ$ είναι ίσα.
(Μονάδες 7)
$Ζ Δ = \frac{Δ Ε}{2}$ .
(Μονάδες 6)

Εμφάνιση Απάντησης

Αρχείο Απάντησης (PDF) Αρχείο Απάντησης (DOC)

ΛΥΣΗ

Έστω τρίγωνο $Α Β Γ$ και τμήματα $Α Δ = Α Β$ , $Α Ε = Α Γ$ στις προεκτάσεις προς το $Α$ των πλευρών $Β Α$ , $Γ Α$ αντίστοιχα.

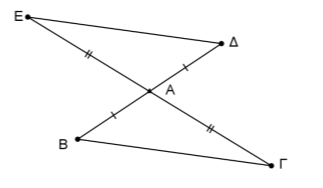
α) Συγκρίνουμε τα τρίγωνα $Α Β Γ$ και $Α Δ Ε$ :

$A Δ = A B$ από υπόθεση,
$A E = A Γ$ από υπόθεση,
$\hat{B Α Γ} = \hat{Δ Α E}$ ως κατακορυφήν

Άρα τα τρίγωνα $Α Β Γ$ και $Α Δ Ε$ είναι ίσα γιατί έχουν δυο πλευρές ίσες μία προς μία και τις περιεχόμενες σε αυτές γωνίες ίσες (κριτήριο $Π Γ Π$ ), οπότε $Β Γ = Δ Ε$ ως πλευρές που βρίσκονται απέναντι από τις ίσες γωνίες $\hat{Β Α Γ}$ και $\hat{Δ Α E}$ των ίσων τριγώνων.

β) Έστω $Α Μ$ η διάμεσος και $Ζ$ το σημείο στο οποίο η προέκτασή της $Α Μ$ τέμνει την $Ε Ζ$ .

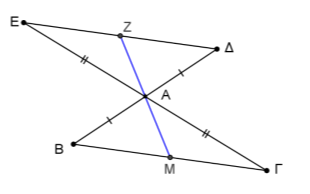
Τα τρίγωνα $Α Β Μ$ και $Α Δ Ζ$ έχουν:
- $Α Β = Α Δ$ από υπόθεση,
- $\hat{B Α M} = \hat{Δ Α Z}$ ως κατακορυφήν γωνίες,
- $\hat{Β} = \hat{Δ}$ , ως γωνίες που βρίσκονται απέναντι από τις ίσες πλευρές $Α Γ$ και $Α Ε$ αντίστοιχα των ίσων τριγώνων $Α Β Γ$ και $Α Δ Ε$ του α) ερωτήματος.
Οπότε τα τρίγωνα $Α Β Μ$ και $Α Δ Ζ$ είναι ίσα γιατί έχουν μια πλευρά και τις προσκείμενες σε αυτή γωνίες ίσες μία προς μία ( $Γ Π Γ$ ).
Από την ισότητα των τριγώνων $Α Β Μ$ και $Α Δ Ζ$ προκύπτει ότι και οι πλευρές που είναι απέναντι από τις ίσες γωνίες τους $\hat{Β Α Μ}$ και $\hat{Δ Α Ζ}$ είναι ίσες, δηλαδή:

$Ζ Δ = Β Μ με Β Μ = \frac{Β Γ}{2}$

Οπότε και $Ζ Δ = \frac{Β Γ}{2} = \frac{Δ Ε}{2}$ διότι είναι $Β Γ = Δ Ε$ από το α) ερώτημα.