ΛΥΣΗ

α) Το τριώνυμο $f(x)=3x^2+9x-12$ έχει $\alpha =3$, $\beta =9$, $\gamma =-12$ και διακρίνουσα:

$$\Delta ={\beta }^2-4\alpha \gamma$$ $$=9^2-4\cdot 3\cdot (-12)$$ $$=81+144=225>0$$

Οι ρίζες του τριωνύμου είναι:

$$x_{\text{1,2}}={\displaystyle \frac{-\beta \pm \sqrt{\Delta }}{2\alpha }}$$ $$={\displaystyle \frac{-9\pm \sqrt{225}}{2\cdot 3}}$$ $$={\displaystyle \frac{-9\pm 15}{6}}$$ $$=\{\begin{array}{l}{\displaystyle \frac{-9+15}{6}}=1\\ {\displaystyle \frac{-9-15}{6}}=-4\end{array}$$

Το πρόσημο του τριωνύμου φαίνεται στον παρακάτω πίνακα:

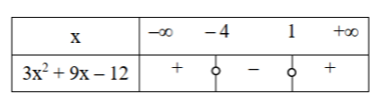
Επομένως ισχύει:

$$f(x)\le 0$$ $$\iff 3x^2+9x-12\le 0$$ $$\iff -4\le x\le 1$$ $$\iff x\in [-4,1]$$

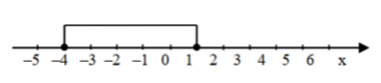
β) Ο αριθμός $\sqrt[3]{2}$ είναι λύση της ανίσωσης αν και μόνο αν:

$$-4\le \sqrt[3]{2}\le 1$$ $$\iff \sqrt[3]{2}\le 1$$ $$\iff (\sqrt[3]{2}{)}^3\le 1^3$$ $$\iff 2\le 1$$

Το οποίο δεν ισχύει. Άρα ο αριθμός $\sqrt[3]{2}$ δεν είναι λύση της ανίσωσης.