Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 12657 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Γεωμετρία | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 36170 | Θέμα: | 2 | |
| Τελευταία Ενημέρωση: | 20-Νοε-2023 | Ύλη: | 3.2. 1ο Κριτήριο ισότητας τριγώνων | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Γεωμετρία | ||
| Θέμα: | 2 | ||
| Κωδικός Θέματος: | 36170 | ||
| Ύλη: | 3.2. 1ο Κριτήριο ισότητας τριγώνων | ||
| Τελευταία Ενημέρωση: 20-Νοε-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 2
Δίνεται ισοσκελές τρίγωνο \(ΑΒΓ\) με \(ΑΒ = ΑΓ\). Στις προεκτάσεις των πλευρών \(ΒΑ\) και \(ΓΑ\) (προς το \(Α\)) θεωρούμε τα σημεία \(Ε\) και \(Δ\) αντίστοιχα τέτοια ώστε \(ΑΕ = ΑΔ\).
Να αποδείξετε ότι:
α) \(ΒΕ = ΓΔ\),
(Μονάδες 6)
β) \(ΒΔ = ΓΕ\),
(Μονάδες 10)
γ) \(\hat{ΔΒΓ}=\hat{ΕΓΒ}\).
(Μονάδες 9)
ΛΥΣΗ
Έστω ισοσκελές τρίγωνο \(ΑΒΓ\) με \(ΑΒ = ΑΓ\) και σημεία \(Ε\), \(Δ\) στις προεκτάσεις των πλευρών \(ΒΑ\), \(ΓΑ\) αντίστοιχα τέτοια ώστε \(ΑΕ =ΑΔ\).
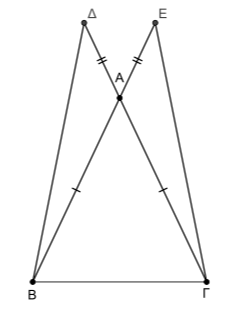
α) Επειδή είναι \(AB = AΓ\) και \(AE = AΔ\) από υπόθεση τότε: \(AB + AE = AΓ + AΔ\), άρα \(BE = ΓΔ\).
β) Τα τρίγωνα \(ΔΒΑ\) και \(ΕΑΓ\) έχουν:
- \(ΑΒ = ΑΓ\), από υπόθεση
- \(ΑΔ = ΑE\), από υπόθεση
- \(\hat{ΔΑΒ} = \hat{ΕΑΓ}\), ως κατακορυφήν γωνίες.
Τα τρίγωνα \(ΔΒΑ\) και \(ΕΑΓ\) έχουν δυο πλευρές ίσες μία προς μία και τις περιεχόμενες σε αυτές γωνίες ίσες, άρα είναι ίσα (\(ΠΓΠ\)), οπότε \(BΔ = ΓE\) ως πλευρές απέναντι από τις ίσες γωνίες \(\hat{ΔΑΒ}\), \(\hat{ΕΑΓ}\) αντίστοιχα.
γ) Τα τρίγωνα \(ΔΒΑ\) και \(ΕΑΓ\) είναι ίσα οπότε: \(\hat{ΔΒΑ}=\hat{ΕΓΑ}\ \ (1)\) ως γωνίες απέναντι από τις ίσες πλευρές \(ΑΔ\) και \(ΑΕ\) αντίστοιχα. Στο ισοσκελές τρίγωνο \(ΑΒΓ\) είναι \(\hat{ΓΒΑ}=\hat{ΒΓΑ}\ \ (2)\), ως γωνίες της βάσης του \(ΒΓ\). Οπότε \(\hat{ΔΒΑ}+ \hat{ΓΒΑ}=\hat{ΕΓΑ}\) + \(\hat{ΒΓΑ}\) ή \(\hat{ΔΒΓ} = \hat{ΕΓΒ}\).
