Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 21513 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Γεωμετρία | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 37124 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 07-Μαρ-2024 | Ύλη: | 3.2. 1ο Κριτήριο ισότητας τριγώνων | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Γεωμετρία | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 37124 | ||
| Ύλη: | 3.2. 1ο Κριτήριο ισότητας τριγώνων | ||
| Τελευταία Ενημέρωση: 07-Μαρ-2024 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
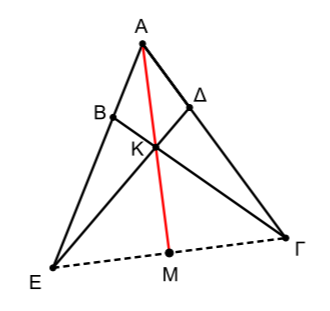
Δίνεται τρίγωνο \(ΑΒΓ\) με \(ΑΒ < ΑΓ\). Στην προέκταση της \(ΑΒ\) (προς το \(Β\)) θεωρούμε σημείο \(Ε\) έτσι ώστε \(ΑΕ = ΑΓ\). Στην πλευρά \(ΑΓ\) θεωρούμε σημείο \(Δ\) έτσι ώστε \(ΑΔ = ΑΒ\). Αν τα τμήματα \(ΔΕ\) και \(ΒΓ\) τέμνονται στο \(Κ\) και η προέκταση της \(ΑΚ\) τέμνει την \(ΕΓ\) στο \(Μ\), τότε να αποδείξετε ότι:
α) \(ΒΓ = ΔΕ\)
(Μονάδες 6)
β) \(ΒΚ = ΚΔ\)
(Μονάδες 7)
γ) Η \(ΑΚ\) είναι διχοτόμος της γωνίας \(Α\).
(Μονάδες 6)
δ) Η \(ΑΜ\) είναι μεσοκάθετος της \(ΕΓ\).
(Μονάδες 6)
ΛΥΣΗ
α) Τα τρίγωνα \(ΒΕΓ\) και \(ΔΕΓ\) έχουν:
- \(ΕΓ\) κοινή
- \(BE = ΔΓ\) ως διαφορά των ίσων τμημάτων \(ΑΕ\), \(ΑΒ\) και \(ΑΓ\), \(ΑΔ\) αντίστοιχα
- \(\hat{ΑΕΓ} = \hat{ΑΓΕ}\), αφού \(ΕΑΓ\) ισοσκελές τρίγωνο
Τα τρίγωνα \(ΒΕΓ\) και \(ΔΕΓ\) έχουν δύο πλευρές ίσες μία προς μία και τις περιεχόμενες γωνίες σε αυτές ίσες άρα είναι ίσα, οπότε έχουν και \(ΒΓ=ΔΕ\) αφού βρίσκονται απέναντι από τις ίσες γωνίες \(\hat{ΑΕΓ}\) και \(\hat{ΑΓΕ}\).
β) Επειδή τα τρίγωνα \(ΒΕΓ\) και \(ΔΕΓ\) είναι ίσα προκύπτει ότι \(\hat{ΔΕΓ} = \hat{ΔΓΕ}\) οπότε το τρίγωνο \(ΚΕΓ\) είναι ισοσκελές, άρα \(ΕΚ= ΚΓ\ \ (1)\).
Τα τρίγωνα \(ΒΕΚ\) και \(ΔΚΓ\) έχουν:
- \(ΕΚ=ΚΓ\), λόγω της \((1)\)
- \(BE=ΔΓ\), ως διαφορές των ίσων τμημάτων \(ΑΕ\), \(ΑΒ\) και \(ΑΓ\), \(ΑΔ\) αντίστοιχα
- \(\hat{ΒΕΚ} = \hat{ΔΓΚ}\) ως διαφορές των ίσων γωνιών \(\hat{ΒΕΓ}\), \(\hat{ΚΕΓ}\) και \(\hat{ΔΓΕ}\), \(\hat{ΚΓΕ}\) αντίστοιχα
Τα τρίγωνα \(ΒΕΚ\) και \(ΔΚΓ\) έχουν δύο πλευρές ίσες μία προς μία και τις περιεχόμενες γωνίες σε αυτές ίσες άρα είναι ίσα, οπότε έχουν και \(ΒΚ=ΚΔ\) αφού βρίσκονται απέναντι από τις ίσες γωνίες \(\hat{ΒΕΚ}\) και \(\hat{ΔΓΚ}\).
γ) Τα τρίγωνα \(ΑΒΚ\) και \(ΑΚΔ\) έχουν:
- \(ΒΚ=ΚΔ\) από το (β) ερώτημα
- \(ΑΚ\) κοινή
- \(ΑΒ=ΑΔ\)
Οπότε τα τρίγωνα \(ΑΒΚ\) και \(ΑΚΔ\) είναι ίσα γιατί έχουν τρεις πλευρές ίσες μία προς μία.
Επομένως \(\hat{ΒΑΚ} = \hat{ΚΑΔ}\) ως γωνίες που βρίσκονται απέναντι από τις ίσες πλευρές \(ΒΚ\) και \(ΚΔ\), οπότε η \(ΑΚ\) είναι διχοτόμος της γωνίας \(\hat{Α}\).
δ) Επειδή το τρίγωνο \(ΑΕΓ\) είναι ισοσκελές και η \(ΑΜ\) είναι διχοτόμος της γωνίας \(\hat{Α}\), θα είναι διάμεσος και ύψος, άρα η \(ΑΜ\) είναι μεσοκάθετος της \(ΕΓ\).