Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
Είστε Μαθηματικός;
Ελάτε στην ομάδα του ΜΕΘΟΔΙΚΟΥ
Ελάτε στην ομάδα του ΜΕΘΟΔΙΚΟΥ
Ευκαιρίες Απασχόλησης
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 32218 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Άλγεβρα | Τάξη: | Β' Λυκείου | |
| Κωδικός Θέματος: | 15024 | Θέμα: | 2 | |
| Τελευταία Ενημέρωση: | 30-Μαρ-2022 | Ύλη: | 2.1 Μονοτονία-Ακρότατα-Συμμετρίες Συνάρτησης | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Β' Λυκείου | ||
| Μάθημα: | Άλγεβρα | ||
| Θέμα: | 2 | ||
| Κωδικός Θέματος: | 15024 | ||
| Ύλη: | 2.1 Μονοτονία-Ακρότατα-Συμμετρίες Συνάρτησης | ||
| Τελευταία Ενημέρωση: 30-Μαρ-2022 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 2
Η γραφική παράσταση μιας συνάρτησης \(f\) με πεδίο ορισμού το \([-4,4]\) φαίνεται στο παρακάτω σχήμα.
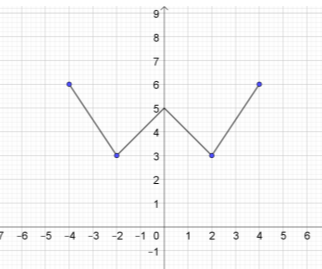
α) Να αιτιολογήσετε γιατί η συνάρτηση είναι άρτια.
(Μονάδες 8)
β) Να βρείτε τα διαστήματα μονοτονίας της \(f.\)
(Μονάδες 8)
γ) Να βρείτε την ελάχιστη τιμή της \(f\) καθώς και για ποιες τιμές του \(x\) την παρουσιάζει.
(Μονάδες 9)
α) Παρατηρούμε ότι η γραφική παράσταση της συνάρτησης \(f\) έχει άξονα συμμετρίας τον \(y'y\), που σημαίνει ότι είναι άρτια.
β) Η συνάρτηση \(f\) είναι γνησίως αύξουσα στο \([-2,0]\) και στο \([2,4]\) και γνησίως φθίνουσα στο \([-4,-2]\) και στο \([0,2].\)
γ) Η \(f\) παρουσιάζει ελάχιστο το \(3\) και οι θέσεις ελαχίστου είναι το \(-2\) και το \(2.\)