Θέμα: 14655

Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!

Τύπος Σχολείου:	Γενικό Λύκειο	Πηγή: Ι.Ε.Π.	Αναγνώσθηκε: 4662 φορές Επικοινωνία
Μάθημα:	Άλγεβρα	Τάξη:	Α' Λυκείου
Κωδικός Θέματος:	14655	Θέμα:	4
Τελευταία Ενημέρωση:	12-Οκτ-2023	Ύλη:	2.2. Διάταξη Πραγματικών Αριθμών 6.1. Η Έννοια της Συνάρτησης
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida)

Τύπος Σχολείου:	Γενικό Λύκειο
Τάξη:	Α' Λυκείου
Μάθημα:	Άλγεβρα
Θέμα:	4
Κωδικός Θέματος:	14655
Ύλη:	2.2. Διάταξη Πραγματικών Αριθμών 6.1. Η Έννοια της Συνάρτησης
Τελευταία Ενημέρωση: 12-Οκτ-2023
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida)

Αρχείο Εκφώνησης (PDF) Αρχείο Εκφώνησης (DOC)

ΘΕΜΑ 4

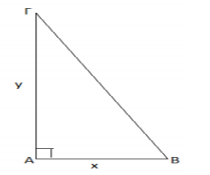
Δίνεται ορθογώνιο τρίγωνο $Α Β Γ$ ( $A = 90^{0}$ ) με κάθετες πλευρές που έχουν μήκη $x$ και $y$ τέτοια, ώστε $x + y = 10$ .

α) Να αποδείξετε ότι το εμβαδόν $Ε$ του ορθογωνίου τριγώνου ως συνάρτηση του $x$ δίνεται από τον τύπο $Ε (x) = \frac{1}{2} (10 x - x^{2})$ με $x \in (0, 10)$ .
(Μονάδες 8)

β)

Να αποδείξετε ότι $Ε (x) \leq \frac{25}{2}$ για κάθε $x \in (0, 10)$ .
(Μονάδες 7)
Για ποια τιμή του $x$ το εμβαδόν γίνεται μέγιστο, δηλαδή ίσο με $\frac{25}{2}$ ;
(Μονάδες 6)

γ) Αν $x = 5$ , ποιο συμπέρασμα προκύπτει για το είδος του τρίγωνου ως προς τις πλευρές του;
(Μονάδες 4)

Εμφάνιση Απάντησης

Αρχείο Απάντησης (PDF) Αρχείο Απάντησης (DOC)

ΛΥΣΗ

α) Επειδή $x$ και $y$ είναι μήκη πλευρών έχουμε $x > 0$ και $y > 0$ με $x + y = 10 \Leftrightarrow y = 10 - x$ .
Από τον τύπο του εμβαδού τριγώνου έχουμε:

$Ε (x) = \frac{1}{2} x \cdot y$ $= \frac{1}{2} x \cdot (10 - x)$ $= \frac{1}{2} (10 x - x^{2})$

με $x \in (0, 10)$ .

β)

Αρκεί να αποδείξουμε την σχέση $Ε (x) \leq \frac{25}{2}$ για κάθε $x \in (0, 10)$ , αρκεί:

$\frac{1}{2} (10 x - x^{2}) \leq \frac{25}{2}$ $\Leftrightarrow 10 x - x^{2} \leq 25$ $\Leftrightarrow x^{2} - 10 x + 25 \geq 0$ $\Leftrightarrow (x - 5)^{2} \geq 0$

ισχύει για $x \in (0, 10)$ .
Tο εμβαδόν γίνεται μέγιστο, δηλαδή ίσο με $\frac{25}{2}$ για $x = 5$ γιατί:

$Ε (x) = \frac{25}{2}$ $\Leftrightarrow \frac{1}{2} (10 x - x^{2}) = \frac{25}{2}$ $\Leftrightarrow (x - 5)^{2} = 0$ $\Leftrightarrow x = 5$

γ) Όταν $x = 5$ τότε $y = 5$ , άρα το τρίγωνο είναι ορθογώνιο ισοσκελές.