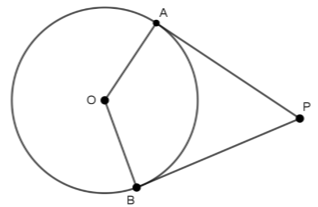
ΛΥΣΗ

α) Τα σημεία ${\rm A}$ και ${\rm B}$ είναι σημεία επαφής των εφαπτόμενων τμημάτων ${\rm P}{\rm A}$ και ${\rm P}{\rm B}$ με τον κύκλο αντίστοιχα και ${\rm O}{\rm A}$, ${\rm O}{\rm B}$ ακτίνες του κύκλου που αντιστοιχούν στα σημεία επαφής.

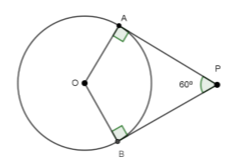
Γνωρίζουμε ότι τα εφαπτόμενα τμήματα από σημείο εκτός κύκλου είναι κάθετα στις ακτίνες που αντιστοιχούν στα σημεία επαφής, οπότε θα είναι $\widehat{{\rm O}{\rm A}{\rm P}}={90}^0$ και $\widehat{{\rm O}{\rm B}{\rm P}}={90}^0$.

Για τις γωνίες του τετράπλευρου ${\rm P}{\rm A}{\rm O}{\rm B}$ ισχύει ότι:
$\widehat{{\rm A}{\rm P}{\rm B}}+\widehat{{\rm O}{\rm B}{\rm P}}+\widehat{{\rm A}{\rm O}{\rm B}}+\widehat{{\rm O}{\rm A}{\rm P}}={360}^0$ ή ${60}^0+{90}^0+\widehat{{\rm A}{\rm O}{\rm B}}+{90}^0={360}^0$
ή $\widehat{{\rm A}{\rm O}{\rm B}}={360}^0-{240}^0$ ή $\widehat{{\rm A}{\rm O}{\rm B}}={120}^0$

β) Φέρνουμε την διακεντρική ευθεία ${\rm P}{\rm O}$.

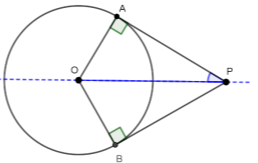
1. Γνωρίζουμε ότι η διακεντρική ευθεία ${\rm P}{\rm O}$ διχοτομεί τη γωνία $\widehat{{\rm A}{\rm P}{\rm B}}$ των εφαπτόμενων τμημάτων ${\rm P}{\rm A}$ και ${\rm P}{\rm B}$, άρα $\widehat{{\rm A}{\rm P}{\rm O}}={\displaystyle \frac{{\rm A}\widehat{{\rm P}}{\rm B}}{2}}={\displaystyle \frac{{60}^0}{2}}={30}^0$.

2. Από το α) ερώτημα έχουμε ότι $\widehat{{\rm O}{\rm A}{\rm P}}={90}^0$, οπότε το τρίγωνο ${\rm O}{\rm A}{\rm P}$ είναι ορθογώνιο. Στο ορθογώνιο τρίγωνο ${\rm O}{\rm A}{\rm P}$ η γωνία $\widehat{{\rm A}{\rm P}{\rm O}}$, λόγω του βi) ερωτήματος, ισούται με ${30}^0$, οπότε η απέναντι κάθετη πλευρά ${\rm A}{\rm O}$ ισούται με το μισό της υποτείνουσας ${\rm P}{\rm O}$, δηλαδή ${\rm O}{\rm A}={\displaystyle \frac{{\rm O}{\rm P}}{2}}$ ή ${\rm O}{\rm P}=2\cdot {\rm O}{\rm A}=2\cdot 4=8cm$.