Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 11157 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Άλγεβρα | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 36673 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 13-Νοε-2023 | Ύλη: | 2.3. Απόλυτη Τιμή Πραγματικού Αριθμού 3.1. Εξισώσεις 1ου Βαθμού | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Άλγεβρα | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 36673 | ||
| Ύλη: | 2.3. Απόλυτη Τιμή Πραγματικού Αριθμού 3.1. Εξισώσεις 1ου Βαθμού | ||
| Τελευταία Ενημέρωση: 13-Νοε-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Σε έναν άξονα τα σημεία \(Α\), \(Β\) και \(Μ\) αντιστοιχούν στους αριθμούς \(5\), \(9\) και \(x\) αντίστοιχα.
α) Να διατυπώσετε τη γεωμετρική ερμηνεία των παραστάσεων \(|x-5|\) και \(|x-9|\).
(Μονάδες 10)
β) Αν ισχύει \(|x-5|=|x-9|\), τότε:
Ποια γεωμετρική ιδιότητα του σημείου \(Μ\) αναγνωρίζετε; Να αιτιολογήσετε τηναπάντησή σας.
(Μονάδες 7)Με χρήση του άξονα, να προσδιορίσετε τον πραγματικό αριθμό \(x\) που παριστάνει το σημείο \(Μ\). Να επιβεβαιώσετε με αλγεβρικό τρόπο την απάντησή σας.
(Μονάδες 8)
ΛΥΣΗ
α) \(|x-5|=d(x,5)=(ΜΑ)\), δηλαδή εκφράζει την απόσταση του σημείου \(Μ\) από το σημείο \(Α\).
\(|x-9|=d(x,9)=(ΜΒ)\), δηλαδή εκφράζει την απόσταση του σημείου \(Μ\) από το σημείο \(Β\).
β)
- Από την ισότητα \(|x-5|=|x-9|\) συμπεραίνουμε ότι \((ΜΑ)=(ΜΒ)\), δηλαδή το σημείο \(Μ\) είναι το μέσο του \(ΑΒ\), όπως φαίνεται και στο παρακάτω σχήμα.
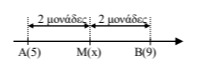
Είναι: \((ΑΒ)=d(5,9)=|5-9)|=|-4|=4\).
Επομένως το σημείο \(Μ\) απέχει \(2\) μονάδες από το σημείο \(Α(5)\) και \(2\) μονάδες από το σημείο \(Β(9)\), οπότε \(x = 7\).
Αλγεβρικά:
$$|x-5|=|x-9| $$ $$\Leftrightarrow x-5=x-9\ \text{ή}\ x-5=-x+9$$ $$x-5=x-9\ \text{αδύνατη ή}\ x-5=-x+9 $$ $$\Leftrightarrow 2x=14 $$ $$\Leftrightarrow x=7$$
